题目内容
19. 如图,已知AD∥BC,P为CD上一点,且AP,BP分别平分∠BAD和∠ABC.
如图,已知AD∥BC,P为CD上一点,且AP,BP分别平分∠BAD和∠ABC.(1)判断△APB是什么三角形,证明你的结论;
(2)比较DP与PC的大小,并说明理由.
分析 (1)通过平行线性质及角平分线性质,可以得到∠APB=90°;
(2)利用中点延长AP与BC交于点E,构造出一对全等三角形△ADP与△ECP,即可以证出DP=PC.
解答 解:(1)△APB是直角三角形
∵AP,BP分别平分∠BAD和∠ABC,
∴∠DAP=∠BAP=$\frac{1}{2}$∠BAD,∠ABP=∠CBP=$\frac{1}{2}$∠ABC,
∵AD∥BC,
∴∠BAD+∠ABC=180°,
∴∠BAP+∠ABP=$\frac{1}{2}$(∠BAD+∠ABC)=90°,
∴∠APB=90°,
∴△APB是直角三角形;
(2)DP=PC
延长AP交BC的延长线于点E,如图: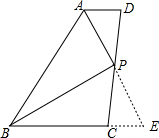 .
.
∵AD∥BC,
∴∠DAP=∠E,
∵∠DAP=∠BAP,
∴∠BAP=∠E,
∴AB=EB,
∵∠APB=90°,
∴AP=PE,
在△ADP与△ECP中,
$\left\{\begin{array}{l}{∠DAP=∠E}\\{AP=EP}\\{∠APD=∠EPC}\end{array}\right.$,
∴△ADP≌△ECP,
∴DP=CP.
点评 本题考查了角平分线性质、平行线性质、全等三角形性质等,解题的关键是利用中点作延长线构建全等三角形.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
7.下列图形中,既是中心对称图形又是轴对称图形的是( )
| A. | 等边三角形 | B. | 直角三角形 | C. | 平行四边形 | D. | 菱形 |
8.下列图表既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
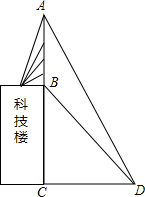 联通公司将移动信号收发塔建在某学校的科技楼上,李明同学利用测倾器在距离科技楼靠塔的一面25米处测得塔顶A的仰角为60°塔底B的仰角为30°,你能利用这些数据帮李明同学计算出该塔的高度吗?($\sqrt{3}$≈1.73,结果精确到0.1米)
联通公司将移动信号收发塔建在某学校的科技楼上,李明同学利用测倾器在距离科技楼靠塔的一面25米处测得塔顶A的仰角为60°塔底B的仰角为30°,你能利用这些数据帮李明同学计算出该塔的高度吗?($\sqrt{3}$≈1.73,结果精确到0.1米)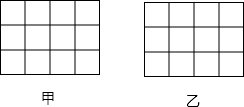 如图,正方形网格中的每个小正方形=边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图.
如图,正方形网格中的每个小正方形=边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图.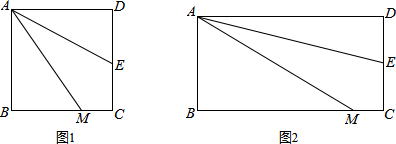
 如图,是将一个长方体沿它的对角线切去一半后剩下的部分.
如图,是将一个长方体沿它的对角线切去一半后剩下的部分.