题目内容
20．正十边形一个内角度数为144°．分析 利用正十边形的外角和是360度，并且每个外角都相等，即可求出每个外角的度数；再根据内角与外角的关系可求出正十边形的每个内角的度数；
解答 解：∵一个十边形的每个外角都相等，
∴十边形的一个外角为360÷10=36°．
∴每个内角的度数为 180°-36°=144°；
故答案为：144°．
点评 本题主要考查了多边形的内角与外角的关系．多边形的外角性质：多边形的外角和是360度．边形的内角与它的外角互为邻补角．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
10．
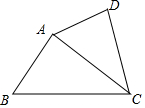如图，在四边形ABCD中，如果∠ADC=∠BAC，那么下列条件中不能判定△ADC和△BAC相似的是（ ）
如图，在四边形ABCD中，如果∠ADC=∠BAC，那么下列条件中不能判定△ADC和△BAC相似的是（ ）| A． | ∠DAC=∠ABC | B． | AC是∠BCD的平分线 | ||
| C． | AC2=BC•CD | D． | $\frac{AD}{AB}$=$\frac{DC}{AC}$ |
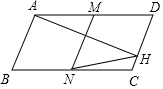如图，在平行四边形ABCD中，AD=2AB，AH⊥CD于H，M为AD的中点，MN∥AB，连接NH，如果∠D=68°，则∠CHN=56°．
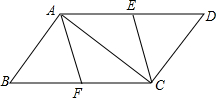如图，?ABCD中，点E、F分别是AD、BC的中点，
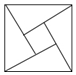我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示），如果大正方形的面积是25，小正方形的面积是1，直角三角形的两直角边分别是a和b，那么ab的值为（ ）
