题目内容
5.某书店销售儿童书刊,一天可售出20套,每套盈利40元,为了扩大销售,增加盈利,尽快减少库存,书店决定采取降价措施.若一套书每降价1元,平均每天可多售出2套.设每套书降价x元时,书店一天可获利润y元.(1)求y关于x的函数表达式.
(2)若要书店每天盈利1200元,则需降价多少元?
(3)当每套书降价多少元时,书店一天可获最大利润?最大利润为多少?
分析 (1)根据题意设出每天降价x元以后,准确表示出每天书刊的销售量,列出利润y关于降价x的函数关系式;
(2)根据题意列出关于x的一元二次方程,通过解方程即可解决问题;
(3)运用函数的性质即可解决.
解答 解:(1)设每套书降价x元时,所获利润为y元,
则每天可出售20+4×$\frac{x}{2}$=20+2x套;
由题意得:y=(40-x)(20+2x)
=-2x2+80x-20x+800
=-2x2+60x+800;
(2)当y=1200时,-2(x-15)2+1250=1200,
整理得:(x-15)2=25,
解得x=10或20但为了尽快减少库存,所以只取x=20,
答:若每天盈利1200元,为了尽快减少库存,则应降价20元;
(3)∵y=-2(x-15)2+1250=1200
则当x=15时,y取得最大值1250;
即当将价15元时,该书店可获得最大利润1250元.
点评 此题考查了二次函数及一元二次方程在现实生活中的应用问题;解题的关键是准确列出二次函数解析式,灵活运用函数的性质解题.

练习册系列答案
相关题目
15. 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹.反弹时反射角等于入射角,当点P第2016次碰到矩形的边时,点P的坐标为( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹.反弹时反射角等于入射角,当点P第2016次碰到矩形的边时,点P的坐标为( )
 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹.反弹时反射角等于入射角,当点P第2016次碰到矩形的边时,点P的坐标为( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹.反弹时反射角等于入射角,当点P第2016次碰到矩形的边时,点P的坐标为( )| A. | (0,3) | B. | (5,0) | C. | (7,4) | D. | (8,3) |
13.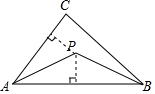 如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB、下列确定P点的方法正确的是( )
如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB、下列确定P点的方法正确的是( )
 如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB、下列确定P点的方法正确的是( )
如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB、下列确定P点的方法正确的是( )| A. | P为∠A、∠B两角平分线的交点 | |
| B. | P为AC、AB两边上的高的交点 | |
| C. | P为∠A的角平分线与AB的垂直平分线的交点 | |
| D. | P为AC、AB两边的垂直平分线的交点 |