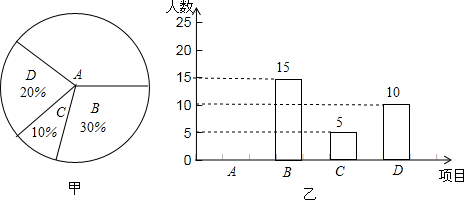
题目内容
15.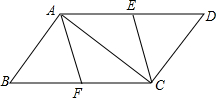 如图,?ABCD中,点E、F分别是AD、BC的中点,
如图,?ABCD中,点E、F分别是AD、BC的中点,(1)求证:四边形AFCE是平行四边形;
(2)若∠BAC=90°,求证:?AFCE是菱形.
分析 (1)根据平行四边形的性质可得AD=BC,AD∥BC,再由点E、F分别是AD、BC的中点可得AE=CF且AE∥CF,从而可根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)根据直角三角形的性质可得AF=CF,再根据一组邻边相等的平行四边形是菱形可得结论.
解答 证明:(1)在?ABCD中,
∴AD=BC,AD∥BC,
∵点E、F分别是AD、BC的中点,
∴AE=CF且AE∥CF,
∴四边形AFCE是平行四边形;
(2)∵∠BAC=90°,点F分别是BC的中点,
∴AF=CF,
∴?AFCE是菱形.
点评 此题主要考查了菱形的判定和平行四边形的判定和性质,关键是掌握平行四边形的判定定理和菱形的判定定理.

练习册系列答案
相关题目
5.|-8|的相反数是( )
| A. | -8 | B. | 8 | C. | $\frac{1}{8}$ | D. | -$\frac{1}{8}$ |
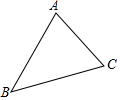 (1)用直尺和圆规作出如图三角形ABC的外接圆⊙O (不写作法,保留作图痕迹).
(1)用直尺和圆规作出如图三角形ABC的外接圆⊙O (不写作法,保留作图痕迹).