Question

10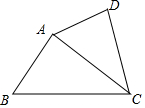．如图，在四边形ABCD中，如果∠ADC=∠BAC，那么下列条件中不能判定△ADC和△BAC相似的是（　　）

• A． ∠DAC=∠ABC
• B． AC是∠BCD的平分线
• C． AC²=BC•CD
• D． $\frac{AD}{AB}$=$\frac{DC}{AC}$

Answer 1

分析 已知∠ADC=∠BAC，则A、B选项可根据有两组角对应相等的两个三角形相似来判定；C选项虽然也是对应边成比例但无法得到其夹角相等，所以不能推出两三角形相似；D选项可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定．

解答 解：在△ADC和△BAC中，∠ADC=∠BAC，
如果△ADC∽△BAC，需满足的条件有：
①∠DAC=∠ABC或AC是∠BCD的平分线；
②$\frac{AD}{AB}$=$\frac{DC}{AC}$；
故选：C．

点评 此题主要考查了相似三角形的判定方法；熟记三角形相似的判定方法是解决问题的关键．