题目内容
15.已知a=$\frac{1}{2+\sqrt{3}}$,求2a2-8a+1的值,小明解决问题的过程如下:∵a=$\frac{1}{2+\sqrt{3}}$=$\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}$=$\frac{2-\sqrt{3}}{{2}^{2}-(\sqrt{3})^{2}}$=2-$\sqrt{3}$.
∴a-2=-$\sqrt{3}$.
∴(a-2)2=3,即a2-4a+4=3
∴a2-4a=-1
∴2a2-8a+1=2(a2-4a)+1=2×(-1)+1=-1
请你根据据小明的解题过程,解决如下问题:
(1)若a=$\frac{1}{\sqrt{2}-1}$,求4a2-8a-3的值;
(2)若m=$\frac{3}{\sqrt{6}+3}$,求-3m2+18m+5的值.
分析 根据阅读材料可得首先利用分式的性质,分子和分母同时乘以与分母相乘能符合平方差公式的式子,去掉分母中的根号即可化简a和m的值,然后把所求的式子进行配方,再代入数值计算即可.
解答 解:(1)a=$\frac{1}{\sqrt{2}-1}$=$\frac{\sqrt{2}+1}{(\sqrt{2}-1)(\sqrt{2}+1)}$=$\sqrt{2}$+1,
原式=4(a-1)2-7=2×($\sqrt{2}$)2-7=4-7=-3;
(2)m=$\frac{3}{\sqrt{6}+3}$=$\frac{3(\sqrt{6}-3)}{(\sqrt{6}+3)(\sqrt{6}-3)}$=3-$\sqrt{6}$,
原式=-3(m2-6m)+5=-3(m-3)2+14=-3(-$\sqrt{6}$)2+14=-18+14=-4.
点评 本题考查了二次根式的化简求值,正确读懂题意,理解化简a和m的方法是关键.

练习册系列答案
相关题目
3.下列运算正确的是( )
| A. | a-1÷a3=a2 | B. | ($\frac{1}{3}$)0=0 | C. | 3-2=$\frac{1}{9}$ | D. | (a2)3=a5 |
20.下列长度的三条线段能构成三角形的是( )
| A. | 3,4,8 | B. | 3,4,7 | C. | 5,6,10 | D. | 5,6,11 |
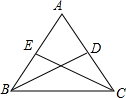 如图,在△ABC中,AB=AC,BD和CE是△ABC的两条角平分线.(请填空)
如图,在△ABC中,AB=AC,BD和CE是△ABC的两条角平分线.(请填空) 如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=1,则AB的长是$\sqrt{3}$.
如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=1,则AB的长是$\sqrt{3}$.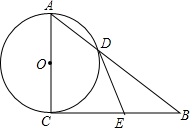 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线交BC于点E.