题目内容
5.将连续的奇数1,3,5,7,…排列成如下的数表,用十字框框住其中的5个数,问: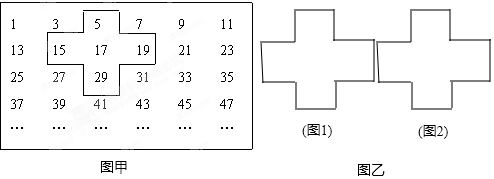
(1)十字框框出5个数的和与框子正中间的数17有什么关系?
(2)若将十字框上下左右平移,可框住另外5个数,若设中间的数为a,用代数式表示十字框框住的5个数字之和;
(3)十字框框住的5个数之和能等于2000吗?若能,请分别写出十字框框住的5个数,并填入图1中.如不能,说明理由.
分析 (1)求出这5个数的和即可得;
(2)若设中间的数为a,则上面的为a-12,下面的为a+12,左面的为a-2,右面的为a+2,据此可得;
(3)根据五个数的和为2000列方程求解后,依据数列为奇数列即可判断.
解答 解:(1)∵5+15+17+19+29=85=17×5,
∴十字框框住的5个数的和是17的5倍;
(2)若设中间的数为a,则上面的为a-12,下面的为a+12,左面的为a-2,右面的为a+2,
∴a+(a-2)+(a+2)+(a-12)+(a+12)=5a;
(3)5个数之和不能等于2000,
当5a=2000时,得a=400,
∵a不是奇数,
∴5个数之和不能等于2000.
点评 本题主要考查列代数式、数字的规律及一元一次方程的应用,根据数列的构成特点得出5个数之间的关系,列出方程依据条件取舍是解题的关键.

练习册系列答案
相关题目
16.化简2(3x-5)+4(3-2x)的结果为( )
| A. | 8x-3 | B. | 2x+9 | C. | -2x+2 | D. | 18x-3 |
13.一次函数y=-2x+6与x轴的交点坐标是( )
| A. | (3,0) | B. | (-3,0) | C. | (0,3) | D. | (0,-3) |
10.一个双肩背书包的标价为a元,现按标价八折出售,则售价是( )
| A. | 8a元 | B. | 2a元 | C. | 0.8a元 | D. | 0.2a元 |
17.一只不透明的袋子中装有7个红球、3个白球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到红球的概率为( )
| A. | $\frac{7}{10}$ | B. | $\frac{7}{3}$ | C. | $\frac{3}{10}$ | D. | $\frac{3}{7}$ |
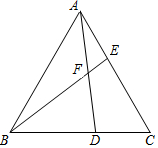 如图,点D、E分别在等边△ABC的边BC、AC上,且AE=CD,AD与BE相交于点F,则∠BFD的度数为60°.
如图,点D、E分别在等边△ABC的边BC、AC上,且AE=CD,AD与BE相交于点F,则∠BFD的度数为60°.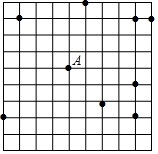 如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为$\sqrt{17}<r≤3\sqrt{2}$.
如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为$\sqrt{17}<r≤3\sqrt{2}$.