题目内容
4.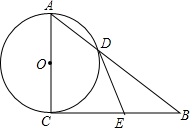 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线交BC于点E.(1)求证:EB=EC;
(2)当△ABC满足什么条件时,四边形ODEC是正方形?证明你的结论.
分析 (1)利用EC为⊙O的切线,ED也为⊙O的切线可求EC=ED,再求得EB=EC,EB=ED可知点E是边BC的中点;
(2)当△ABC是等腰直角三角形时,四边形ODEC是正方形,由等腰三角形的性质,得到∠ODA=∠A=45°,于是∠DOC=90°然后根据有一组邻边相等的矩形是正方形,即可得到结论.
解答  解:
解:
(1)证明:连接CD,
∵AC是直径,∠ACB=90°,
∴BC是⊙O的切线,∠ADC=90°.
∵DE是⊙O的切线,
∴DE=CE(切线长定理).
∴∠DCE=∠CDE,
又∵∠DCE+∠EBD=∠CDE+∠EDB=90°,
∴∠EBD=∠EDB.
∴DE=BE,
∴CE=BE.
(2)当△ABC是等腰直角三角形时,四边形ODEC是正方形.理由如下:
∵△ABC是等腰直角三角形.
∴∠B=45°,
∴∠DCE=∠CDE=45°,则∠DEB=90°,
又∵OC=OD,∠ACB=90°,
∴∠OCD=∠ODC=45°,
∴∠ODE=90°,
∴四边形ODEC是矩形,
∵EC=ED,
∴四边形ODEC是正方形.
点评 本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
16.如果正比例函数y=kx的图象经过点(-1,3),则当x=2时,函数y的值为( )
| A. | -6 | B. | -$\frac{2}{3}$ | C. | 6 | D. | $\frac{2}{3}$ |
13.若点P(3,2m-1)在第四象限,则m的取值范围是( )
| A. | m>$\frac{1}{2}$ | B. | m<$\frac{1}{2}$ | C. | m≥-$\frac{1}{2}$ | D. | m≤$\frac{1}{2}$ |
14.下列分解因式正确的是( )
| A. | x2+2x+1=x(x+2)+1 | B. | (x2-4)x=x3-4x | C. | ax+bx=(a+b)x | D. | m2-2mn+n2=(m-n)2 |
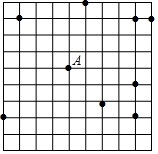 如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为$\sqrt{17}<r≤3\sqrt{2}$.
如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为$\sqrt{17}<r≤3\sqrt{2}$.