题目内容
6.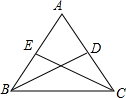 如图,在△ABC中,AB=AC,BD和CE是△ABC的两条角平分线.(请填空)
如图,在△ABC中,AB=AC,BD和CE是△ABC的两条角平分线.(请填空)求证:BD=CE
证明:
∵AB=AC (已知 )
∴∠ABC=∠ACB
∵BD,CE分别是∠ABC,∠ACB的平分线 (已知)
∴∠CBD=$\frac{1}{2}$∠ABC,
∠BCE=$\frac{1}{2}$∠ACB角平分线定义
∴∠CBD=∠BCE
又∵BC=CB (公共边)
∴△BCE≌△CBDASA
∴BD=CE(全等三角形的对应角相等.
分析 根据条件只要证明△BCE≌△CBD,写出理由即可解决问题.
解答 解:∵AB=AC (已知 )
∴∠ABC=∠ACB
∵BD,CE分别是∠ABC,∠ACB的平分线 (已知)
∴∠CBD=$\frac{1}{2}$∠ABC,∠BCE=$\frac{1}{2}$∠ACB (角平分线定义)
∴∠CBD=∠BCE,
又∵BC=CB (公共边)
∴△BCE≌△CBD (ASA)
∴BD=CE 全等三角形对应边相等).
故答案分别为∠ACB,$\frac{1}{2}$,$\frac{1}{2}$,角平分线定义,∠BCE,ASA,全等三角形的对应边相等.
点评 本题考查全等三角形的判定和性质、角平分线的定义等知识,解题的关键是正确寻找全等三角形,属于基础题,中考常考题型.

练习册系列答案
相关题目
16.化简2(3x-5)+4(3-2x)的结果为( )
| A. | 8x-3 | B. | 2x+9 | C. | -2x+2 | D. | 18x-3 |
17.一只不透明的袋子中装有7个红球、3个白球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到红球的概率为( )
| A. | $\frac{7}{10}$ | B. | $\frac{7}{3}$ | C. | $\frac{3}{10}$ | D. | $\frac{3}{7}$ |
1.已知关于x的分式方程$\frac{a+2}{x+1}$=1的解是非正数,则a的取值范围是( )
| A. | a≤-1 | B. | a≤1且a≠-2 | C. | a≤-1且a≠-2 | D. | a≤1 |
18.已知方程x2k-1+3=0是关于x的一元一次方程,则k的值等于( )
| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
16.如果正比例函数y=kx的图象经过点(-1,3),则当x=2时,函数y的值为( )
| A. | -6 | B. | -$\frac{2}{3}$ | C. | 6 | D. | $\frac{2}{3}$ |
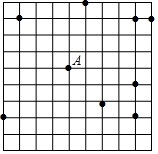 如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为$\sqrt{17}<r≤3\sqrt{2}$.
如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为$\sqrt{17}<r≤3\sqrt{2}$.