题目内容
6.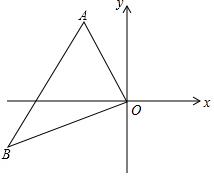 如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点B的对应点B′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点B的对应点B′的坐标是( )| A. | (-3,-1) | B. | (-1,2) | C. | (-9,1)或(9,-1) | D. | (-3,-1)或(3,1) |
分析 利用以原点为位似中心,相似比为k,位似图形对应点的坐标的比等于k或-k,把B点的横纵坐标分别乘以$\frac{1}{3}$或-$\frac{1}{3}$即可得到点B′的坐标.
解答 解:∵以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,
∴点B(-9,3)的对应点B′的坐标是(-3,-1)或(3,1).
故选D.
点评 本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.

练习册系列答案
相关题目
1.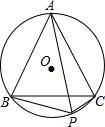 如图,等边△ABC是⊙O的内接三角形,P是$\widehat{BC}$上一点,当PB=3PC时,则△ABC与四边形ABPC的面积比为( )
如图,等边△ABC是⊙O的内接三角形,P是$\widehat{BC}$上一点,当PB=3PC时,则△ABC与四边形ABPC的面积比为( )
 如图,等边△ABC是⊙O的内接三角形,P是$\widehat{BC}$上一点,当PB=3PC时,则△ABC与四边形ABPC的面积比为( )
如图,等边△ABC是⊙O的内接三角形,P是$\widehat{BC}$上一点,当PB=3PC时,则△ABC与四边形ABPC的面积比为( )| A. | $\frac{13}{16}$ | B. | $\frac{10}{13}$ | C. | $\frac{9}{11}$ | D. | $\frac{7}{9}$ |
18.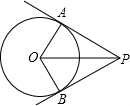 如图,PA,PB是⊙O的两条切线,切点分别是A,B,如果OP=4,PA=2$\sqrt{3}$,那么∠APB等于( )
如图,PA,PB是⊙O的两条切线,切点分别是A,B,如果OP=4,PA=2$\sqrt{3}$,那么∠APB等于( )
 如图,PA,PB是⊙O的两条切线,切点分别是A,B,如果OP=4,PA=2$\sqrt{3}$,那么∠APB等于( )
如图,PA,PB是⊙O的两条切线,切点分别是A,B,如果OP=4,PA=2$\sqrt{3}$,那么∠APB等于( )| A. | 90° | B. | 100° | C. | 110° | D. | 60° |
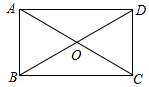 如图,在矩形ABCD中,∠ABD=60°,AB=4,则AC=8.
如图,在矩形ABCD中,∠ABD=60°,AB=4,则AC=8. 如图,将一张长方形的纸片ABCD沿AF折叠,点B到达点B′的位置.已知AB′∥BD,∠ADB=20°,则∠BAF=55°.
如图,将一张长方形的纸片ABCD沿AF折叠,点B到达点B′的位置.已知AB′∥BD,∠ADB=20°,则∠BAF=55°.