题目内容
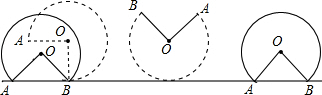
11.观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,…,按此规律,图形n中星星的颗数是$\frac{1}{2}{n}^{2}$+$\frac{5}{2}$n-1(用含n的代数式表示)
分析 设图形n中星星的颗数是an(n为正整数),列出部分图形中星星的个数,根据数据的变化找出变化规律$\frac{1}{2}{n}^{2}$+$\frac{5}{2}$n-1”,依此规律即可得出结论.
解答 解:设图形n中星星的颗数是an(n为正整数),
∵a1=2=1+1,a2=6=(1+2)+3,a3=11=(1+2+3)+5,a4=17=(1+2+3+4)+7,
∴an=1+2+…+n+(2n-1)=$\frac{n(n+1)}{2}$+(2n-1)=$\frac{1}{2}{n}^{2}$+$\frac{5}{2}$n-1,
故答案为:$\frac{1}{2}{n}^{2}$+$\frac{5}{2}$n-1.
点评 本题考查了规律型中的图形的变化类,根据图形中数的变化找出变化规律是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.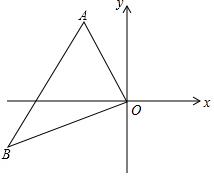 如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点B的对应点B′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点B的对应点B′的坐标是( )
 如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点B的对应点B′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点B的对应点B′的坐标是( )| A. | (-3,-1) | B. | (-1,2) | C. | (-9,1)或(9,-1) | D. | (-3,-1)或(3,1) |
3.计算(-5)×(-1)的结果等于( )
| A. | 5 | B. | -5 | C. | 1 | D. | -1 |
20.计算2$\sqrt{\frac{1}{2}}$-$\sqrt{18}$的结果是( )
| A. | -$\sqrt{2}$ | B. | -2$\sqrt{2}$ | C. | -4$\sqrt{2}$ | D. | -8$\sqrt{2}$ |
1. 如图,AB∥EF∥CD,∠ABC=44°,∠CEF=154°,则∠BCE等于( )
如图,AB∥EF∥CD,∠ABC=44°,∠CEF=154°,则∠BCE等于( )
 如图,AB∥EF∥CD,∠ABC=44°,∠CEF=154°,则∠BCE等于( )
如图,AB∥EF∥CD,∠ABC=44°,∠CEF=154°,则∠BCE等于( )| A. | 22° | B. | 18° | C. | 20° | D. | 26° |
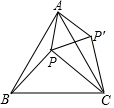 如图,点P是等边△ABC内一点,连接PA,PB,PC,PA:PB:PC=3:4:5,以AC为边作△AP′C≌△APB,连接PP′,则有以下结论:①△APP′是等边三角形;②△PCP′是直角三角形;③∠APB=150°;④∠APC=105°.其中一定正确的是①②③.(把所有正确答案的序号都填在横线上)
如图,点P是等边△ABC内一点,连接PA,PB,PC,PA:PB:PC=3:4:5,以AC为边作△AP′C≌△APB,连接PP′,则有以下结论:①△APP′是等边三角形;②△PCP′是直角三角形;③∠APB=150°;④∠APC=105°.其中一定正确的是①②③.(把所有正确答案的序号都填在横线上)