题目内容
6.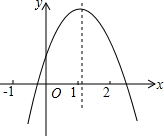 二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-2b,则( )
二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-2b,则( )| A. | M>0,N>0,P>0 | B. | M>0,N<0,P<0 | C. | M<0,N>0,P>0 | D. | M<0,N>0,P<0 |
分析 把x=2代入抛物线解析式得到M的符号;把x=-1代入函数解析式求得n的符号;根据对称轴的位置得到P的符号.
解答 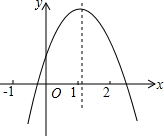 解:如图所示,当x=2时,y>0,即M=4a+2b+c>0,所以M>0.
解:如图所示,当x=2时,y>0,即M=4a+2b+c>0,所以M>0.
当x=-1时,y<0,即N=a-b+c<0,所以N<0.
如图所示,抛物线开口方向向下,则a<0,
对称轴在y轴的右侧,则a、b异号,即b>0,
所以由对称轴x=-$\frac{b}{2a}$>1,得到:2a>-b,
所以0>4a-2b>-4b>0.即P<0.
综上所述,M>0,N>0,P<0.
故选:B.
点评 本题考查了二次函数图象与系数的关系.会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换.

练习册系列答案
相关题目
17.已知M是关于x的五次多项式,N是关于x的三次多项式,则下列说法中正确的是( )
| A. | M+N是关于x的八次多项式 | B. | M-N是关于x的二次多项式 | ||
| C. | M+N与M-N都是关于x的五次多项式 | D. | M+N与M-N是几次多项式无法确定 |
18.已知函数y=ax2+bx+c(a≠0)的图象开口向上,并且经过(-1,-2),(1,0).下列结论中,正确的是( )
| A. | 当x>0,函数y随x值的增大而增大 | |
| B. | 当x>0,函数y随x值的增大而减小 | |
| C. | 存在一个负数x0,使得x<x0,函数y随x值的增大而减小;当x>x0时,函数y随x值的增大而增大 | |
| D. | 存在一个正数x0,使得x<x0,函数y随x值的增大而减小;当x>x0时,函数y随x值的增大而增大 |
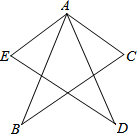 已知,如图,AE=AC,∠E=∠C,∠EAB=∠CAD,求证:AB=AD.
已知,如图,AE=AC,∠E=∠C,∠EAB=∠CAD,求证:AB=AD.