题目内容
14.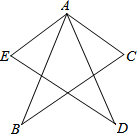 已知,如图,AE=AC,∠E=∠C,∠EAB=∠CAD,求证:AB=AD.
已知,如图,AE=AC,∠E=∠C,∠EAB=∠CAD,求证:AB=AD.
分析 证明它们所在的三角形全等即可,由∠EAB=∠CAD可得∠CAB=∠EAD,运用AAS证明△ABC≌△ADE.
解答 证明:∵∠EAB=∠CAD,
∴∠EAB+∠EAC=∠CAD+∠CAE,
即∠CAB=∠EAD.
在△ABC和△ADE中,
$\left\{\begin{array}{l}{∠C=∠E}\\{∠CAB=∠EAD}\\{AE=AC}\end{array}\right.$,
∴△ABC≌△ADE,
∴AB=AD.
点评 此题考查全等三角形的判定与性质,属基础题.证明线段相等,可证明它们所在的三角形全等.

练习册系列答案
相关题目
4.下列说法中正确的是( )
| A. | 多项式x+32次数是2 | B. | 多项式-x2+2x-1的项为x2,2x,-1 | ||
| C. | 多项式$\frac{x-2}{4}$的常数项为-2 | D. | 多项式2x2y-x是三次二项式 |
5.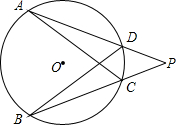 如图,∠P=40°,$\widehat{AB}$=$\widehat{BC}$=$\widehat{DA}$,∠CAD等于( )
如图,∠P=40°,$\widehat{AB}$=$\widehat{BC}$=$\widehat{DA}$,∠CAD等于( )
 如图,∠P=40°,$\widehat{AB}$=$\widehat{BC}$=$\widehat{DA}$,∠CAD等于( )
如图,∠P=40°,$\widehat{AB}$=$\widehat{BC}$=$\widehat{DA}$,∠CAD等于( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
6.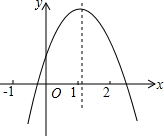 二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-2b,则( )
二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-2b,则( )
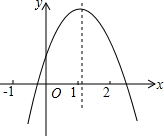 二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-2b,则( )
二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-2b,则( )| A. | M>0,N>0,P>0 | B. | M>0,N<0,P<0 | C. | M<0,N>0,P>0 | D. | M<0,N>0,P<0 |
 如图,已知线段a,b,c,求作△ABC,使AB=a-b,AC=b,BC=c.
如图,已知线段a,b,c,求作△ABC,使AB=a-b,AC=b,BC=c.