题目内容

17．已知M是关于x的五次多项式，N是关于x的三次多项式，则下列说法中正确的是（　　）
A．M+N是关于x的八次多项式B．M-N是关于x的二次多项式
C．M+N与M-N都是关于x的五次多项式D．M+N与M-N是几次多项式无法确定

分析 根据多项式和同类项的概念可知：五次三项式中的五次项没有同类项，所以不能合并，即所得结果仍为五次多项式．

解答 解：∵M是关于x的五次多项式，N是关于x的三次多项式，M中没有关于x的五次单项式的同类项，
∴M+N，M-N结果中x的次数就不会改变，就是5，
∴M+N与M-N都是关于x的五次多项式．
故选：C．

点评 此题考查多项式，解决此类题目的关键是熟记整式的加减只能是同类项间的加减，非同类项之间不能进行合并．

练习册系列答案
相关题目
7．如果（-2am）n=-2namn（a≠0），那么n是（　　）
A．正数B．正奇数C．正偶数D．自然数
8．有这样一道题：“当a=999，b=9999时，求多项式7a3-6a3b+3a2b+3a2+6a3b-3a2b-10a3的值．”小明说：本题中a，b的值这么大，怎么好算呢？小强说：本题中a=999，b=9999是多余的条件；小红马上反对说：这不可能，多项式中每一项都含有a和b，不给出a，b的值怎么能求出多项式的值呢？你同意谁的观点？请说明理由．
5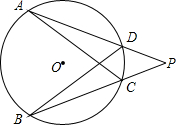．如图，∠P=40°，$\widehat{AB}$=$\widehat{BC}$=$\widehat{DA}$，∠CAD等于（　　）
A．10°B．15°C．20°D．30°
12．下列结论正确的有（　　）
①若$\frac{a}{b}$=$\frac{c}{d}$，则$\frac{a+2b}{b}$=$\frac{c+2d}{d}$；②若$\frac{a}{b}$=$\frac{c}{d}$，则$\frac{a+1}{b}$=$\frac{c+1}{d}$；③若$\frac{a}{b}$=$\frac{c}{d}$，则$\frac{a-c}{c}$=$\frac{b-d}{d}$；④若$\frac{a}{b+c}$=$\frac{b}{a+c}$=$\frac{c}{a+b}$=k，则k=$\frac{1}{2}$．
A．1个B．2个C．3个D．4个
2．求出函数y=x（8-x）的顶点坐标和对称轴以及函数的最大值或最小值．
9．计算：
（1）$\frac{4a+4b}{5ab}$•$\frac{35{a}^{2}b}{{a}^{2}-{b}^{2}}$；
（2）$\frac{{x}^{2}-4{y}^{2}}{{x}^{2}+4x+4}$•$\frac{x+2}{3{x}^{2}+6xy}$；
（3）$\frac{{x}^{2}+1}{x-6}$•$\frac{{x}^{2}-36}{{x}^{3}+x}$；
（4）$\frac{{y}^{2}-{x}^{2}}{5{x}^{2}-4xy}$÷$\frac{x+y}{5x-4y}$；
（5）$\frac{4{x}^{2}-4xy+{y}^{2}}{2x+y}$÷（4x2-y2）；
（6）$\frac{9{y}^{2}-{x}^{2}}{{x}^{2}+6xy+9{y}^{2}}$÷$\frac{x-3y}{{x}^{2}+3xy}$．
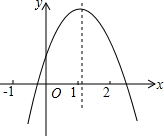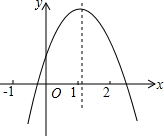6．二次函数y=ax2+bx+c的图象如图所示，若M=4a+2b+c，N=a-b+c，P=4a-2b，则（　　）
A．M＞0，N＞0，P＞0B．M＞0，N＜0，P＜0C．M＜0，N＞0，P＞0D．M＜0，N＞0，P＜0
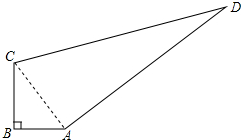7．如图，在四边形ABCD中，∠B=90°，AB=3，BC=4，CD=7，AD=8，求这个四边形的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网