题目内容
18.已知函数y=ax2+bx+c(a≠0)的图象开口向上,并且经过(-1,-2),(1,0).下列结论中,正确的是( )| A. | 当x>0,函数y随x值的增大而增大 | |
| B. | 当x>0,函数y随x值的增大而减小 | |
| C. | 存在一个负数x0,使得x<x0,函数y随x值的增大而减小;当x>x0时,函数y随x值的增大而增大 | |
| D. | 存在一个正数x0,使得x<x0,函数y随x值的增大而减小;当x>x0时,函数y随x值的增大而增大 |
分析 根据二次函数的图象与性质逐一分析探讨得出答案即可..
解答 解:根据二次函数y=ax2+bx+c(a≠0)的图象开口向上,并经过点(-1,-2),(1,0).
将(-1,-2)代入函数解析式得:a-b+c=-2①,
将(1,0)代入函数解析式得:a+b+c=0②,
②-①得:2b=-2,解得:b=-1<0,
又∵抛物线开口向上,可得a>0,
∴-$\frac{b}{2a}$>0,
则函数的对称轴x>0.
所以A、B、C不正确;D正确.
故选:D.
点评 此题考查了二次函数的性质以及对称轴的判定.要先确定对称轴才能判断图象的单调性.

练习册系列答案
相关题目
6.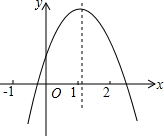 二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-2b,则( )
二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-2b,则( )
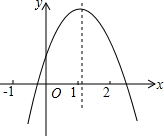 二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-2b,则( )
二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-2b,则( )| A. | M>0,N>0,P>0 | B. | M>0,N<0,P<0 | C. | M<0,N>0,P>0 | D. | M<0,N>0,P<0 |
10.下列说法中错误的是( )
| A. | 优弧大于劣弧 | B. | 半径相等的两个半圆是等弧 | ||
| C. | 同圆或等圆的半径相等 | D. | 能够互阳重合的弧是等弧 |
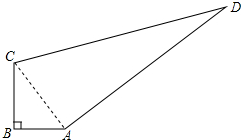 如图,在四边形ABCD中,∠B=90°,AB=3,BC=4,CD=7,AD=8,求这个四边形的面积.
如图,在四边形ABCD中,∠B=90°,AB=3,BC=4,CD=7,AD=8,求这个四边形的面积.