题目内容
12．
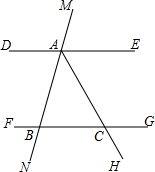已知如图，直线MN分别与直线DE、FG相交于A、B两点，∠MAD=128°，∠NBF=52°．（1）直线DE与FG平行吗？说明理由；
（2）若射线AH平分∠BAE且交FG于C，求∠FCH的度数．
分析 （1）先根据补角的定义求出∠DAB的度数，进而可得出结论；
（2）由角平分线的性质得出∠BAC的度数，再由平行线的性质即可得出结论．
解答 解：（1）平行．
理由：∵∠MAD=128°，
∴∠DAB=180°-128°=52°．
∵∠NBF=52°，
∴DE∥FG．
（2）∵∠BAE=∠MAD=128°，AH平分∠BAE，
∴∠BAC=$\frac{1}{2}$×128°=64°，
∴∠DAC=52°+64°=116°．
∵DE∥FG，
∴∠FCH=∠DAC=116°．
点评 本题考查的是平行线的判定定理，用到的知识点为：同位角相等，两直线平行．
练习册系列答案
相关题目
如图，⊙O的直径AB=4，AC是弦，沿AC折叠劣弧$\widehat{AB}$，记折叠后的劣弧为$\widehat{AmC}$，当$\widehat{AmC}$经过圆心O时，图中阴影部分的面积为$\sqrt{3}$；当$\widehat{AmC}$与直径AB交于点D时，设AC=x，BD=y，则y关于x的函数关系式为y=-$\frac{1}{2}$x2+8．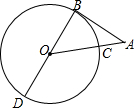
如图，BD为⊙O的直径，AB与⊙O相切于点B，连结AO，AO与⊙O交于点C，若∠A=40°，⊙O的半径为2，则$\widehat{CD}$的长为$\frac{13}{9}$π．
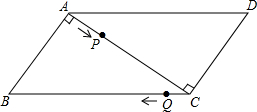已知，如图，用两块一样大的直角三角板拼成一个平行四边形，∠BAC=∠ACD=90°．在?ABCD中，AB=3cm，BC=5cm，点P自A向C、沿AC的方向匀速运动，速度为1cm/s；同时，点Q从点C出发，自C向B、沿CB方向匀速运动，速度为1cm/s；过点P作PM⊥AD，并与AD相交于点M，当P、Q中有一个点到达终点时，另一个点也停止运动．设运动时间为t（s）．解答下列问题：
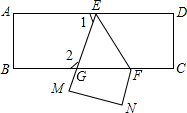如图，把一张长方形纸片ABCD沿EF折叠，折叠后点D与M点重合，点C与点N重合，EM与BC相交于点G，若∠AEM=52°，则∠EFG=64°．
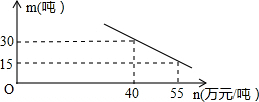某口生产一种产品，当产量至少为10吨，但不超过55吨时，每吨的成本y（万元）与产量x（吨）之间是一次函数关系：y=-0.5x+50．