题目内容
1. 某口生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本y(万元)与产量x(吨)之间是一次函数关系:y=-0.5x+50.
某口生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本y(万元)与产量x(吨)之间是一次函数关系:y=-0.5x+50.(1)当投入生产这种产品的总成本为1200万元时,求该产品的总产量;(注:总成本=每吨成本×总产量)
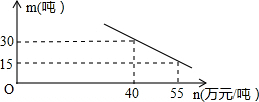
(2)市场调查发现,这种产品每月销售m(吨)与销售单价n(万元/吨)之间满足如图所示的函数关系式,该厂第一月按同一销售单价卖出这种产品25吨,请求出该厂第一个月销售这种产品获得的利润.(注:利润=售价-成本)
分析 (1)由总成本=每吨成本×总产量,结合每吨的成本y(万元)与产量x(吨)之间是一次函数关系:y=-0.5x+50可得出关于x的一元二次方程,解方程即可得出结论;
(2)设m关于n的解析式为m=kn+b,结合图象上的点的坐标利用待定系数法即可求出m关于n的解析式,将m=25,x=25分别代入两个解析式中即可求出每吨的成本及每吨的售价,结合利润=售价-成本即可得出结论.
解答 解:(1)由已知得xy=1200,
将y=-0.5x+50代入xy=1200中得x(-0.5x+50)=1200,
解得:x=40,或x=60>55(舍去).
答:当投入生产这种产品的总成本为1200万元时,该产品的总产量为40吨.
(2)设m关于n的解析式为m=kn+b,
将点(40,30)和(55,15)代入m=kn+b中得:
$\left\{\begin{array}{l}{30=40k+b}\\{15=55k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-1}\\{b=70}\end{array}\right.$.
∴m=-n+70.
令m=25,则有25=-n+70,解得:n=45.
令x=25,则y=-0.5×25+50=37.5.
该厂第一个月销售这种产品获得的利润为m(n-y)=25×(45-37.5)=187.5(万元).
答:该厂第一月按同一销售单价卖出这种产品25吨,则该厂第一个月销售这种产品获得的利润为187.5万元.
点评 本题考查了一次函数的应用以及一元二次方程的应用,解题的关键:(1)根据数量关系找出关于x的一元二次方程;(2)利用待定系数法求出m关于n的函数解析式.本题属于中档题,难度不大,解决该题型题目时,根据数量关系找出方程(方程组或函数关系式)是关键.

 阅读快车系列答案
阅读快车系列答案| A. | 28.09×108 | B. | 2.809×108 | C. | 28.09×109 | D. | 2.809×109 |
| A. | 2.037×1010元 | B. | 2.037×1011元 | C. | 2.037×1012元 | D. | 20.37×1010元 |
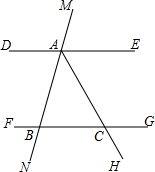 已知如图,直线MN分别与直线DE、FG相交于A、B两点,∠MAD=128°,∠NBF=52°.
已知如图,直线MN分别与直线DE、FG相交于A、B两点,∠MAD=128°,∠NBF=52°.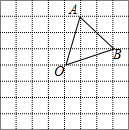 如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别是A(1,3),B(3,1).
如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别是A(1,3),B(3,1).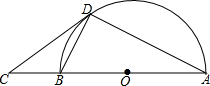 如图,AB是半圆O的直径,C是AB延长线上一点,CD与半圆O相切于点D,连接AD,BD.
如图,AB是半圆O的直径,C是AB延长线上一点,CD与半圆O相切于点D,连接AD,BD.