题目内容
4.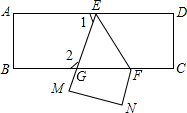 如图,把一张长方形纸片ABCD沿EF折叠,折叠后点D与M点重合,点C与点N重合,EM与BC相交于点G,若∠AEM=52°,则∠EFG=64°.
如图,把一张长方形纸片ABCD沿EF折叠,折叠后点D与M点重合,点C与点N重合,EM与BC相交于点G,若∠AEM=52°,则∠EFG=64°.
分析 直接利用翻折变换的性质以及结合平行线的性质得出∠DEF=∠MEF的度数,进而得出答案.
解答 解:∵把一张长方形纸片ABCD沿EF折叠,折叠后点D与M点重合,点C与点N重合,
∴∠DEF=∠MEF,
∵∠AEM=52°,
∴∠DEF=∠MEF=$\frac{1}{2}$×(180°-52°)=64°,
∵AB∥BC,
∴∠DEF=∠EFG=64°.
故答案为:64°.
点评 此题主要考查了平行线的性质以及翻折变换的性质,正确得出∠DEF=∠MEF的度数是解题关键.

练习册系列答案
相关题目
19. 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )
如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )
 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )
如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )| A. | $\frac{π+\sqrt{2}-1}{2}$cm2 | B. | $\frac{2}{3}$πcm2 | C. | $\frac{4π+3\sqrt{3}-3}{6}$cm2 | D. | $\frac{π+\sqrt{3}-1}{2}$cm2 |
 如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点E,过点D作DF∥BE交AC于点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点E,过点D作DF∥BE交AC于点F.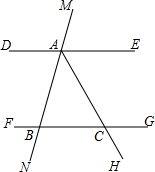 已知如图,直线MN分别与直线DE、FG相交于A、B两点,∠MAD=128°,∠NBF=52°.
已知如图,直线MN分别与直线DE、FG相交于A、B两点,∠MAD=128°,∠NBF=52°.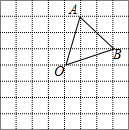 如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别是A(1,3),B(3,1).
如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别是A(1,3),B(3,1).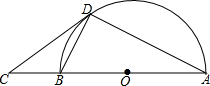 如图,AB是半圆O的直径,C是AB延长线上一点,CD与半圆O相切于点D,连接AD,BD.
如图,AB是半圆O的直径,C是AB延长线上一点,CD与半圆O相切于点D,连接AD,BD.