题目内容
7.计算:①$3\sqrt{2}-4\sqrt{2}+5\sqrt{2}$ ②$3\frac{1}{8}×4\sqrt{3}÷\sqrt{\frac{2}{3}}$
③$\sqrt{27}-\sqrt{8}-\sqrt{48}+\sqrt{18}$ ④$\sqrt{20}+(1-\sqrt{3})^{0}-\sqrt{80}×{2}^{-1}$.
分析 ①直接合并同类二次根式即可;
②利用二次根式的除法法则运算;
③先把各二次根式化为最简二次根式,然后合并即可;、
④根据零指数幂和负整数指数幂的意义计算.
解答 解:①原式=4$\sqrt{2}$;
②原式=$\frac{25}{8}$×4×$\sqrt{3×\frac{3}{2}}$
=$\frac{75\sqrt{2}}{4}$;
③原式=3$\sqrt{3}$-2$\sqrt{2}$-4$\sqrt{3}$+3$\sqrt{2}$
=$\sqrt{2}$-$\sqrt{3}$;
④原式=2$\sqrt{5}$+1-4$\sqrt{5}$×$\frac{1}{2}$
=2$\sqrt{5}$+1-2$\sqrt{5}$
=1.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
19. 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )
如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )
 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )
如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )| A. | $\frac{π+\sqrt{2}-1}{2}$cm2 | B. | $\frac{2}{3}$πcm2 | C. | $\frac{4π+3\sqrt{3}-3}{6}$cm2 | D. | $\frac{π+\sqrt{3}-1}{2}$cm2 |
 如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点E,过点D作DF∥BE交AC于点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点E,过点D作DF∥BE交AC于点F.
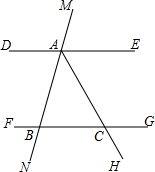 已知如图,直线MN分别与直线DE、FG相交于A、B两点,∠MAD=128°,∠NBF=52°.
已知如图,直线MN分别与直线DE、FG相交于A、B两点,∠MAD=128°,∠NBF=52°.