题目内容
2. 如图,⊙O的直径AB=4,AC是弦,沿AC折叠劣弧$\widehat{AB}$,记折叠后的劣弧为$\widehat{AmC}$,当$\widehat{AmC}$经过圆心O时,图中阴影部分的面积为$\sqrt{3}$;当$\widehat{AmC}$与直径AB交于点D时,设AC=x,BD=y,则y关于x的函数关系式为y=-$\frac{1}{2}$x2+8.
如图,⊙O的直径AB=4,AC是弦,沿AC折叠劣弧$\widehat{AB}$,记折叠后的劣弧为$\widehat{AmC}$,当$\widehat{AmC}$经过圆心O时,图中阴影部分的面积为$\sqrt{3}$;当$\widehat{AmC}$与直径AB交于点D时,设AC=x,BD=y,则y关于x的函数关系式为y=-$\frac{1}{2}$x2+8.
分析 如图1,作半径OE⊥AC于F,如图1,根据折叠的性质得OF=$\frac{1}{2}$OE=1,由OE⊥AC,根据垂径定理得AF=CF,再在Rt△OAF中,利用勾股定理计算出AF=$\sqrt{3}$,所以AC=2AF=2$\sqrt{3}$,然后根据扇形和三角形的面积公式计算即可;如图2,设弧AMC所在圆的圆心为P,作PH⊥AB于H,连结OP、PD、BC,由于点P和点O关于AC对称,得到AC垂直平分OP,在Rt△PAH中,PH=$\sqrt{P{A}^{2}-A{H}^{2}}$=$\sqrt{2y-\frac{1}{4}{y}^{2}}$,在Rt△OPH中,OP=$\sqrt{P{H}^{2}+O{H}^{2}}$=$\sqrt{2y}$,推出OP∥BC,由平行线的性质得到∠POH=∠CBA,证得Rt△ACB∽Rt△PHO,根据相似三角形的性质得到结论.
解答 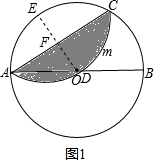 解:作半径OE⊥AC于F,如图1,
解:作半径OE⊥AC于F,如图1,
∵沿AC折叠劣弧$\widehat{AC}$,记折叠后的劣弧为$\widehat{AmC}$.
∴OF=$\frac{1}{2}$OE=$\frac{1}{2}$×2=1,
∴∠AOF=60°,∴∠ADC=120°,
∵OE⊥AC,
∴AF=CF,
在Rt△OAF中,OA=2,OF=1,
∴AF=$\sqrt{O{A}^{2}-O{F}^{2}}$=$\sqrt{3}$,
∴AC=2AF=2$\sqrt{3}$,
∴S阴影=S扇形OAEC-S△AOC=$\frac{120π×{2}^{2}}{360}$=$\frac{1}{2}×$2$\sqrt{3}$×1=$\sqrt{3}$;
设弧AMC所在圆的圆心为P,
作PH⊥AB于H,连结OP、PD、BC,如图2,
∵点P和点O关于AC对称,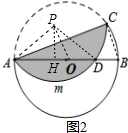
∴AC垂直平分OP,
∴AP=AO=2,
∵AB=4,BD=y,
∴AD=4-y,
∵PH⊥AD,
∴AH=DH=$\frac{1}{2}$AD=2-$\frac{1}{2}$y,
∴OH=OA-AH=$\frac{1}{2}$y,
在Rt△PAH中,PH=$\sqrt{P{A}^{2}-A{H}^{2}}$=$\sqrt{2y-\frac{1}{4}{y}^{2}}$,
在Rt△OPH中,OP=$\sqrt{P{H}^{2}+O{H}^{2}}$=$\sqrt{2y}$,
∵沿AC折叠劣弧$\widehat{AC}$,记折叠后的劣弧为$\widehat{AmC}$,
∴OP⊥AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴OP∥BC,
∴∠POH=∠CBA,
∴Rt△ACB∽Rt△PHO,
∴$\frac{AC}{PH}=\frac{AB}{PO}$,
∴AC=$\frac{4•\sqrt{2y-\frac{1}{4}{y}^{2}}}{\sqrt{2y}}$=$\sqrt{16-2y}$,
∴y=-$\frac{1}{2}$x2+8.
故答案为:$\sqrt{3}$,y=-$\frac{1}{2}$x2+8.
点评 本题考查了垂径定理、圆周角定理和切线的性质;会利用勾股定理和相似比进行几何计算;理解折叠的性质和正方形的判定与性质.

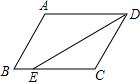 如图,在?ABCD中,AD=8cm,AB=6cm,DE平分∠ADC,交BC边于点E,则BE的长为( )
如图,在?ABCD中,AD=8cm,AB=6cm,DE平分∠ADC,交BC边于点E,则BE的长为( )| A. | 2cm | B. | 4cm | C. | 6cm | D. | 8cm |
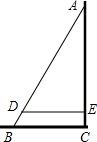 如图,AB是斜靠在墙上的长梯,梯脚B距墙脚1.6m,梯上点D距墙1.4m,BD长0.55m,求该梯子的长.
如图,AB是斜靠在墙上的长梯,梯脚B距墙脚1.6m,梯上点D距墙1.4m,BD长0.55m,求该梯子的长.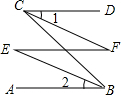 如图,已知AB∥CD,试再添上一个条件,就可证明∠1=∠2,试用两种方法证明.
如图,已知AB∥CD,试再添上一个条件,就可证明∠1=∠2,试用两种方法证明. 如图,∠1=∠ACB,∠2=∠3,证明:CD∥FH.
如图,∠1=∠ACB,∠2=∠3,证明:CD∥FH.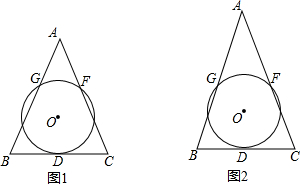
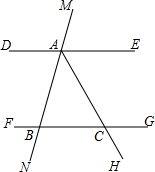 已知如图,直线MN分别与直线DE、FG相交于A、B两点,∠MAD=128°,∠NBF=52°.
已知如图,直线MN分别与直线DE、FG相交于A、B两点,∠MAD=128°,∠NBF=52°.