题目内容
13．若点A（2，-3），B（4，3），C（5，m）在同一条直线上，则m=6．分析 先利用待定系数法求出直线的解析式，然后根据一次函数图象上点的坐标特征，把C（5，m）代入所求的解析式即可得到m的值．
解答 解：设直线解析式为y=kx+b，
把A（2，-3），B（4，3）代入得$\left\{\begin{array}{l}{2k+b=-3}\\{4k+b=3}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=3}\\{b=-9}\end{array}\right.$，
所以直线解析式为y=3x-9，
把C（5，m）代入得m=3×5-9=6．
故答案为6．
点评 本题考查了一次函数图象上点的坐标特征：一次函数y=kx+b，（k≠0，且k，b为常数）的图象是一条直线．它与x轴的交点坐标是（-$\frac{b}{a}$，0）；与y轴的交点坐标是（0，b）．直线上任意一点的坐标都满足函数关系式y=kx+b．
练习册系列答案
阅读快车系列答案
相关题目
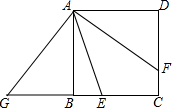如图，在正方形ABCD中，E为BC上一点，AF平分∠DAE交CD于点F，反向延长BC至G，使BG=DF，连接AG，求证：
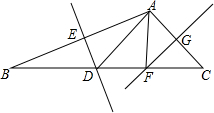如图，在△ABC中，∠C=45°，DE垂直平分AB于点E，交BC于点D；FG垂直平分AC于点G，交BC于点F，连接AD，AF．若AC=3$\sqrt{2}$cm，BC=12cm，则DF=4cm．
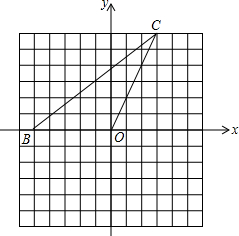已知：如图，在平面直角坐标系中，点B（-5，0），点C（3，6），若点D是由点C平移得到，并且△OBD与△OBC的面积相等，请写出三个不同的点D的坐标．
已知?ABCD中，对角线AC、BD相交于点O，∠ABD=2∠CBD，AE⊥BD．求证：AB=2EO．