题目内容
3.设k≠$\frac{1}{2}$,求证:不论k取何值,直线y=(2k-1)x+(k-1)总经过一个定点.分析 把直线y=(2k-1)x+(k-1)化为y=(2k-1)x+(k-1)=(2x+1)k-x-1的形式,再令k的系数等于求出x的值,进而可得出结论.
解答 解:∵y=(2k-1)x+(k-1)
=2kx-x+k-1
=(2x+1)k-x-1,
∴当2x+1=0,即x=-$\frac{1}{2}$时,y=-$\frac{1}{2}$,
即不论k取何值,直线y=(2k-1)x+(k-1)总经过定点(-$\frac{1}{2}$,-$\frac{1}{2}$).
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
8.在直角坐标系内,下列结论成立的是( )
| A. | 点(4,3)与点(3,4)表示同一个点 | |
| B. | 平面内的任一点到两坐标轴的距离相等 | |
| C. | 若点P(x,y)的坐标满足xy=0,则点P在坐标轴上 | |
| D. | 点P(m,n)到x轴的距离为m,到y轴的距离为n |
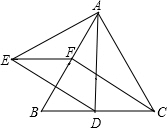 如图,△ABC与△ADE都是等边三角形,CD=BF,求证:四边形CDEF是平行四边形.
如图,△ABC与△ADE都是等边三角形,CD=BF,求证:四边形CDEF是平行四边形.