题目内容
4.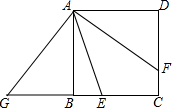 如图,在正方形ABCD中,E为BC上一点,AF平分∠DAE交CD于点F,反向延长BC至G,使BG=DF,连接AG,求证:
如图,在正方形ABCD中,E为BC上一点,AF平分∠DAE交CD于点F,反向延长BC至G,使BG=DF,连接AG,求证:(1)△ADF≌△ABG;
(2)AE=BE+DF.
分析 (1)由正方形的性质可得AB=AD,∠D=∠ABG=90°,又因为BG=DF,所以可以证明△ADF≌△ABG;
(2)由(1)可知BG=DF,由图形可知GE=BE+BG,所以要证明AE=BE+DF,只要证明GE=AE即可.
解答  证明:(1)∵四边形ABCD是正方形,
证明:(1)∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABG=90°,
在△ADF和△ABG中,
$\left\{\begin{array}{l}{AD=AB}\\{∠D=∠ABG=90°}\\{DF=BG}\end{array}\right.$,
∴△ADF≌△ABG;
(2)∵△ADF≌△ABG,
∴DF=BG,∠DAF=∠GAB,∠G=∠AFD,
∵AB∥DC,
∴∠AFD=∠BAF,
∵AF平分∠DAE,
∴∠DAF=∠FAE,
∴∠GAE=∠F,
∴∠G=∠GAE,
∴AE=GE,
∴GE=BE+BG=DF+BE,
∴AE=BE+DF.
点评 本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,等腰三角形的性质的运用,角平分线的判定的运用,解答时通过证明三角形全等是关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
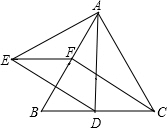 如图,△ABC与△ADE都是等边三角形,CD=BF,求证:四边形CDEF是平行四边形.
如图,△ABC与△ADE都是等边三角形,CD=BF,求证:四边形CDEF是平行四边形. 如图,已知O是△ABC内的一点,试说明:
如图,已知O是△ABC内的一点,试说明: