题目内容
1.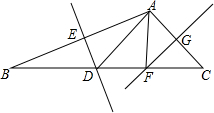 如图,在△ABC中,∠C=45°,DE垂直平分AB于点E,交BC于点D;FG垂直平分AC于点G,交BC于点F,连接AD,AF.若AC=3$\sqrt{2}$cm,BC=12cm,则DF=4cm.
如图,在△ABC中,∠C=45°,DE垂直平分AB于点E,交BC于点D;FG垂直平分AC于点G,交BC于点F,连接AD,AF.若AC=3$\sqrt{2}$cm,BC=12cm,则DF=4cm.
分析 根据线段的垂直平分线的性质得到FA=FC,DA=DB,根据直角三角形的判定得到∠AFC=90°,设DF=x,根据勾股定理列出方程,解方程得到答案.
解答 解:∵FG垂直平分AC,
∴FA=FC,
∴∠FAC=∠C=45°,
∴∠AFC=90°,又FA=FC,
∴FA=FC=3,
∵DE垂直平分AB,
∴DA=DB,
设DF=x,则DA=DB=9-x,
由勾股定理得(9-x)2=x2+32,
解得,x=4,
故答案为:4.
点评 本题考查的是线段的垂直平分线的性质和勾股定理,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
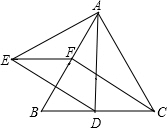 如图,△ABC与△ADE都是等边三角形,CD=BF,求证:四边形CDEF是平行四边形.
如图,△ABC与△ADE都是等边三角形,CD=BF,求证:四边形CDEF是平行四边形. 如图,△ABC的两条高AD、CE相交于点M,已知∠BAC=30°,∠ACB=75°,求∠AMC的度数.
如图,△ABC的两条高AD、CE相交于点M,已知∠BAC=30°,∠ACB=75°,求∠AMC的度数.