题目内容
9.计算:(1)$\frac{4a+4b}{5ab}$•$\frac{35{a}^{2}b}{{a}^{2}-{b}^{2}}$;
(2)$\frac{{x}^{2}-4{y}^{2}}{{x}^{2}+4x+4}$•$\frac{x+2}{3{x}^{2}+6xy}$;
(3)$\frac{{x}^{2}+1}{x-6}$•$\frac{{x}^{2}-36}{{x}^{3}+x}$;
(4)$\frac{{y}^{2}-{x}^{2}}{5{x}^{2}-4xy}$÷$\frac{x+y}{5x-4y}$;
(5)$\frac{4{x}^{2}-4xy+{y}^{2}}{2x+y}$÷(4x2-y2);
(6)$\frac{9{y}^{2}-{x}^{2}}{{x}^{2}+6xy+9{y}^{2}}$÷$\frac{x-3y}{{x}^{2}+3xy}$.
分析 (1)首先将分子与分母因式分解,进而化简求出即可;
(2)首先将分子与分母因式分解,进而化简求出即可;
(3)首先将分子与分母因式分解,进而化简求出即可;
(4)首先将分子与分母因式分解,再利用分式除法运算法则进而化简求出即可;
(5)首先将分子与分母因式分解,再利用分式除法运算法则进而化简求出即可;
(6)首先将分子与分母因式分解,再利用分式除法运算法则进而化简求出即可.
解答 解:(1)$\frac{4a+4b}{5ab}$•$\frac{35{a}^{2}b}{{a}^{2}-{b}^{2}}$
=$\frac{4(a+b)}{5ab}$×$\frac{35{a}^{2}b}{(a+b)(a-b)}$
=$\frac{28a}{a-b}$;
(2)$\frac{{x}^{2}-4{y}^{2}}{{x}^{2}+4x+4}$•$\frac{x+2}{3{x}^{2}+6xy}$
=$\frac{(x+2y)(x-2y)}{(x+2)^{2}}$×$\frac{x+2}{3x(x+2y)}$
=$\frac{x-2y}{3{x}^{2}+6x}$;
(3)$\frac{{x}^{2}+1}{x-6}$•$\frac{{x}^{2}-36}{{x}^{3}+x}$
=$\frac{{x}^{2}+1}{x-6}$×$\frac{(x+6)(x-6)}{x({x}^{2}+1)}$
=$\frac{x+6}{x}$;
(4)$\frac{{y}^{2}-{x}^{2}}{5{x}^{2}-4xy}$÷$\frac{x+y}{5x-4y}$
=$\frac{(y-x)(y+x)}{x(5x-4y)}$×$\frac{5x-4y}{x+y}$
=$\frac{y-x}{x}$;
(5)$\frac{4{x}^{2}-4xy+{y}^{2}}{2x+y}$÷(4x2-y2)
=$\frac{(2x-y)^{2}}{2x+y}$×$\frac{1}{(2x+y)(2x-y)}$
=$\frac{2x-y}{4{x}^{2}+4xy+{y}^{2}}$;
(6)$\frac{9{y}^{2}-{x}^{2}}{{x}^{2}+6xy+9{y}^{2}}$÷$\frac{x-3y}{{x}^{2}+3xy}$
=$\frac{(3y-x)(3y+x)}{(x+3y)^{2}}$×$\frac{x(x+3y)}{x-3y}$
=x.
点评 此题主要考查了分式的乘除运算,正确分解因式是解题关键.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案| A. | M+N是关于x的八次多项式 | B. | M-N是关于x的二次多项式 | ||
| C. | M+N与M-N都是关于x的五次多项式 | D. | M+N与M-N是几次多项式无法确定 |
| A. | 当x>0,函数y随x值的增大而增大 | |
| B. | 当x>0,函数y随x值的增大而减小 | |
| C. | 存在一个负数x0,使得x<x0,函数y随x值的增大而减小;当x>x0时,函数y随x值的增大而增大 | |
| D. | 存在一个正数x0,使得x<x0,函数y随x值的增大而减小;当x>x0时,函数y随x值的增大而增大 |
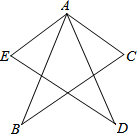 已知,如图,AE=AC,∠E=∠C,∠EAB=∠CAD,求证:AB=AD.
已知,如图,AE=AC,∠E=∠C,∠EAB=∠CAD,求证:AB=AD.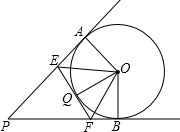 如图所示,PA,PB是⊙O的切线,切点分别是点A,B.点Q为AB上一点.过点Q作⊙O的切线,分别交PA,PB于E,F两点.已知PA=12cm,∠P=56°.
如图所示,PA,PB是⊙O的切线,切点分别是点A,B.点Q为AB上一点.过点Q作⊙O的切线,分别交PA,PB于E,F两点.已知PA=12cm,∠P=56°.