题目内容
19.x=$\frac{1}{2}$时,多项式-2x+x+$\frac{1}{2}$x+$\frac{1}{3}$x的值是-$\frac{1}{12}$.分析 原式合并同类项后,将x的值代入计算即可求出值.
解答 解:原式=(-2+1+$\frac{1}{2}$+$\frac{1}{3}$)x=-$\frac{1}{6}$x,
当x=$\frac{1}{2}$时,原式=-$\frac{1}{12}$.
故答案为:-$\frac{1}{12}$.
点评 此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
10.下列式子:2a2b,x-y,$\frac{x+2}{a}$,$\frac{a+b}{2}$,-2x-1,x+$\frac{1}{x}$,a+$\frac{b}{2}$,-m2.其中是多项式的有( )
| A. | 2个 | B. | 4个 | C. | 6个 | D. | 8个 |
7.如果(-2am)n=-2namn(a≠0),那么n是( )
| A. | 正数 | B. | 正奇数 | C. | 正偶数 | D. | 自然数 |
4.下列说法中正确的是( )
| A. | 多项式x+32次数是2 | B. | 多项式-x2+2x-1的项为x2,2x,-1 | ||
| C. | 多项式$\frac{x-2}{4}$的常数项为-2 | D. | 多项式2x2y-x是三次二项式 |
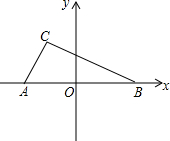 在△ABC中,∠ACB=90°,∠BAC=60°,AC=2,如图,以AB所在的直线为x轴,以AB的垂直平分线为y轴,建立直角坐标系,求点A、B、C的坐标.
在△ABC中,∠ACB=90°,∠BAC=60°,AC=2,如图,以AB所在的直线为x轴,以AB的垂直平分线为y轴,建立直角坐标系,求点A、B、C的坐标.