题目内容
7.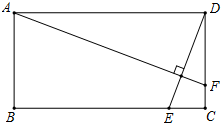 如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F.设DF=x,EC=y.
如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F.设DF=x,EC=y.(1)求y关于x的函数关系式,并写出x的取值范围.
(2)当CF=1时,求EC的长.
(3)若直线AF与线段BC延长线交于点G,当△DBE与△DFG相似时,求DF的长.
分析 (1)易证△ADF∽△DCE,然后运用相似三角形的性质即可得到y与x的关系,然后根据y的范围就可得到x的范围;
(2)由于点F的位置不确定,需分点F在线段DC及点F在线段DC的延长线上两种情况进行讨论,然后利用y与x的关系即可解决问题;
(3)由∠DEC=∠AFD=90-∠EDC可得∠BED=∠DFG,因而在△DBE和△DFG中,点E与点F是对应点,故当△DBE与△DFG相似时,可分△DEB∽△GFD和△DEB∽△DFG两种情况进行讨论,然后只需用x的代数式表示ED、FG、EB,再运用相似三角形的性质即可解决问题.
解答 解:(1)如图1,
∵四边形ABCD是矩形,
∴DC=AB=2,∠ADC=∠BCD=90°.
又∵AF⊥DE,
∴∠ADF=∠DCE=90°,∠DAF=∠EDC=90°-∠DFA,
∴△ADF∽△DCE,
∴$\frac{AD}{DC}$=$\frac{DF}{CE}$,
∴$\frac{4}{2}$=$\frac{x}{y}$,即y=$\frac{1}{2}$x.
∵点E在线段BC上,与点B、C不重合,
∴0<y<4,∴0<$\frac{1}{2}$x<4,即0<x<8,
∴y=$\frac{1}{2}$x,(0<x<8);
(2)①当点F线段DC上时,
∵CF=1,
∴DF=x=2-1=1,此时CE=y=$\frac{1}{2}$x=$\frac{1}{2}$;
②当点F线段DC延长线上时,
∵CF=1,
∴DF=x=2+1=3,此时CE=y=$\frac{1}{2}$x=$\frac{3}{2}$;
∴当CF=1时,EC的长为$\frac{1}{2}$或$\frac{3}{2}$;
(3)在Rt△ADF中,AF=$\sqrt{A{D}^{2}+D{F}^{2}}$=$\sqrt{16+{x}^{2}}$,
在Rt△DCE中,DE=$\sqrt{E{C}^{2}+D{C}^{2}}$=$\sqrt{(\frac{1}{2}x)^{2}+4}$=$\frac{1}{2}$$\sqrt{16+{x}^{2}}$,
∵四边形ABCD是矩形,
∴AD∥BC,
∴△ADF∽△GCF,
∴$\frac{AF}{GF}$=$\frac{DF}{CF}$,
∴FG=$\frac{CF•AF}{DF}$=$\frac{2-x}{x}\sqrt{{x^2}+16}$.
∵∠DEC=∠AFD=90-∠EDC,
∴∠BED=∠DFG,
∴当△DBE与△DFG相似时,可分以下两种情况讨论:
①△DEB∽△GFD,如图2,
则有$\frac{ED}{EB}$=$\frac{FG}{FD}$,
∴ED•FD=FG•EB,
∴$\frac{1}{2}\sqrt{{x^2}+16}$•x=$\frac{2-x}{x}\sqrt{{x^2}+16}$•(4-$\frac{1}{2}$x),
解得:x=$\frac{8}{5}$.
②若△DEB∽△DFG,如图3,
则有$\frac{ED}{EB}$=$\frac{FD}{FG}$,
∴ED•FG=EB•FD,
∴$\frac{1}{2}\sqrt{{x^2}+16}$•$\frac{2-x}{x}\sqrt{{x^2}+16}$=(4-$\frac{1}{2}$x)•x,
整理得:3x2+8x-16=0,
解得:x1=$\frac{4}{3}$,x2=-4(舍去).
综上所述:DF的长为$\frac{8}{5}$或$\frac{4}{3}$.
点评 本题主要考查了矩形的性质、相似三角形的判定与性质、解方程等知识,对运算能力的要求比较高,当点的位置不确定、相似三角形的对应关系不确定时,常常需要分类讨论,避免出现漏解的现象.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案| A. | -$\sqrt{3.6}$=-0.6 | B. | $\root{3}{-5}$=-$\root{3}{5}$ | C. | $\sqrt{(-13)^{2}}$=-13 | D. | $\sqrt{36}$=±6 |
| A. | 5 | B. | 4 | C. | 3 | D. | 1 |
| A. | 扩大3倍 | B. | 不变 | C. | 缩小3倍 | D. | 缩小6倍 |
| A. | k≥-2 | B. | k≤-2 | C. | k≥2 | D. | k≤2 |
 如图,在△ABC中,AB=AC,D为边BC上一点,以AB、BD为邻边作平行四边形ABDE,连接AD、EC.若BD=CD,求证:四边形ADCE是矩形.
如图,在△ABC中,AB=AC,D为边BC上一点,以AB、BD为邻边作平行四边形ABDE,连接AD、EC.若BD=CD,求证:四边形ADCE是矩形. 如图,在平面直角坐标系中,A(0,2),M(-4,0),点B从点M出发,速度为每秒k个单位,同时点P从原点O出发,速度为每秒1个单位,点B与点P都沿x轴正方向向右运动.设运动时间为t秒.动点Q在反比例函数y=$\frac{4}{x}$的图象上.
如图,在平面直角坐标系中,A(0,2),M(-4,0),点B从点M出发,速度为每秒k个单位,同时点P从原点O出发,速度为每秒1个单位,点B与点P都沿x轴正方向向右运动.设运动时间为t秒.动点Q在反比例函数y=$\frac{4}{x}$的图象上.