题目内容
2. 如图,在平面直角坐标系中,A(0,2),M(-4,0),点B从点M出发,速度为每秒k个单位,同时点P从原点O出发,速度为每秒1个单位,点B与点P都沿x轴正方向向右运动.设运动时间为t秒.动点Q在反比例函数y=$\frac{4}{x}$的图象上.
如图,在平面直角坐标系中,A(0,2),M(-4,0),点B从点M出发,速度为每秒k个单位,同时点P从原点O出发,速度为每秒1个单位,点B与点P都沿x轴正方向向右运动.设运动时间为t秒.动点Q在反比例函数y=$\frac{4}{x}$的图象上.(1)当k=1,t=1时,直接写出点B,点P的坐标;
(2)当k=2时,是否存在点Q,使得以A,B,Q,P为顶点的四边形是平行四边形,如果存在,请直接写出Q点坐标,并求出此时t的值;如果不存在,说明理由;
(3)探索在运动过程中,以A,B,Q,P为顶点的四边形是平行四边形时t和k应满足的关系式.
分析 (1)利用速度公式计算出BM和OP,则可得到点B,点P的坐标;
(2)当k=2时,BM=2t,OP=t,B(2t-4,0),P(t,0),则PB=t-(2t-4)=3t-4,分类讨论:
当点Q在第一象限,如图1,利用平行四边形的性质得AQ∥PB,AQ=PB,则Q点的纵坐标为2,则可确定Q(2,2),所以PB=AQ=2,即t-(2t-4)=2,再解方程求出t的值;
当点Q在第三象限,如图2,连结AQ交x轴与D,根据平行四边形的性质得DA=DQ,OB=OP,易得Q(-2,-2),D(-1,0),利用DP=DQ得到t+1=-1-(2t-4),再解方程求出t的值;
(3)B(kt-4,0),PB=4-(k-1)t,与(2)类似,分类讨论:当点Q在第一象限,利用PB=PQ=2得到4-(k-1)t=2,所以t=$\frac{2}{k-1}$;当点Q在第三象限,如图2,连结AQ交x轴与D,利用DP=DQ得到t+1=-1-(kt-4),解得t=$\frac{2}{k+1}$.
解答 解:(1)当k=1,t=1,则BM=1,OP=1,
所以B(-3,0),P(1,0);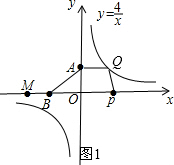 (2)存在.
(2)存在.
当k=2时,BM=2t,OP=t,B(2t-4,0),P(t,0),
则PB=t-(2t-4)=3t-4,
当点Q在第一象限,如图1,
∵四边形ABPQ为平行四边形,
∴AQ∥PB,AQ=PB,
∴Q点的纵坐标为2,
当y=2时,$\frac{4}{x}$=2,解得x=2,则Q(2,2),
∴PB=AQ=2,
即t-(2t-4)=2,解得t=2;
当点Q在第三象限,如图2,连结AQ交x轴与D,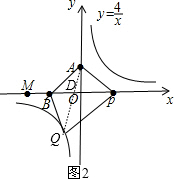
∵四边形ABPQ为平行四边形,
∴DA=DQ,OB=OP,
∴Q点的纵坐标为-2,
当y=-2时,$\frac{4}{x}$=-2,解得x=-2,则Q(-2,-2),
∴D(-1,0),
∴t+1=-1-(2t-4),解得t=$\frac{2}{3}$,
即满足条件的t的值为2或$\frac{2}{3}$;
(3)BM=kt,OP=t,B(kt-4,0),P(t,0),
则PB=t-(kt-4)=4-(k-1)t,
当点Q在第一象限,由(2)得到Q(2,2),由于PB=PQ=2,则4-(k-1)t=2,所以t=$\frac{2}{k-1}$;
当点Q在第三象限,如图2,连结AQ交x轴与D,由(2)得到Q(-2,-2),D(-1,0),由DP=DQ得到t+1=-1-(kt-4),解得t=$\frac{2}{k+1}$.
点评 本题考查了反比例函数综合题:熟练掌握反比例函数图象上点的坐标特征和平行四边形的判定方法;会运用分类讨论的思想解决问题;通过用代数式表示相应相等来解决动点问题.

 名校课堂系列答案
名校课堂系列答案| A. | -6 | B. | -2.5 | C. | 2 | D. | 不能确定 |
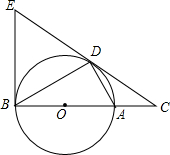 如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD.
如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD.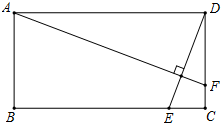 如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F.设DF=x,EC=y.
如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F.设DF=x,EC=y. 如图,⊙O的直径AB交弦CD于点P,请你添加一个条件:AP⊥CD,使得CP=DP.
如图,⊙O的直径AB交弦CD于点P,请你添加一个条件:AP⊥CD,使得CP=DP.