题目内容
15．若点（5，2）在一次函数y=kx-3（k≠0）的图象上，则k的值是（ ）| A． | 5 | B． | 4 | C． | 3 | D． | 1 |
分析 把点（5，2）代入一次函数y=kx-3，通过解一元一次方程来求k的值．
解答 解：∵一次函数y=kx-3的图象经过点（5，2），
∴5k-3=2，
解得 k=1．
故选：D．
点评 本题考查了一次函数图象上点的坐标特征．直线上任意一点的坐标都满足函数关系式y=kx+b（k≠0）．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
6．下列说法中不正确的是（ ）
| A． | 抛掷一枚硬币，硬币落地时正面朝上是随机事件 | |
| B． | 把4个球放入三个抽屉中，其中一个抽屉中至少有2个球是必然事件 | |
| C． | 任意打开七年级下册数学教科书，正好是97页是确定事件 | |
| D． | 在相同条件下，只要试验的次数足够多，频率就可以作为概率的估计值 |
3．
如图，在Rt△ABC中，∠C=90°，∠A=30°，AC=2，则AB=（ ）
如图，在Rt△ABC中，∠C=90°，∠A=30°，AC=2，则AB=（ ）| A． | 4 | B． | $\frac{2\sqrt{3}}{3}$ | C． | $\frac{4\sqrt{3}}{3}$ | D． | $\frac{\sqrt{3}}{3}$ |
20．
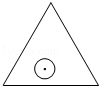如图，一个半径为r的圆形纸片在边长为a$（a≥2\sqrt{3}r）$的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片“不能接触到的部分”的面积是（ ）
如图，一个半径为r的圆形纸片在边长为a$（a≥2\sqrt{3}r）$的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片“不能接触到的部分”的面积是（ ）| A． | $（3\sqrt{3}-π）{r^2}$ | B． | $\frac{{（3\sqrt{3}-π）}}{3}{r^2}$ | C． | $\frac{π}{3}{r^2}$ | D． | πr2 |
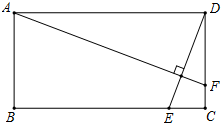如图，矩形ABCD中，AB=2，AD=4，动点E在边BC上，与点B、C不重合，过点A作DE的垂线，交直线CD于点F．设DF=x，EC=y．
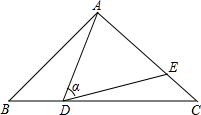如图，在△ABC中，AB=AC=10，点D是边BC上一动点（不与B，C重合），∠ADE=∠B=α，DE交AC于点E，且cosα=$\frac{4}{5}$．下列结论：①△ADE∽△ACD；②当BD=6时，△ABD与△DCE全等；③△DCE为直角三角形时，BD为8；④0＜CE≤6.4．其中正确的结论是①②④．（把你认为正确结论的序号都填上）