题目内容
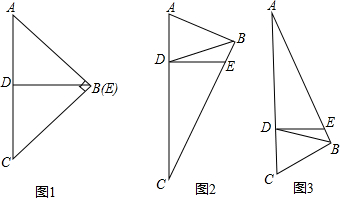
18．
如图，在△ABC中，AB=AC，D为边BC上一点，以AB、BD为邻边作平行四边形ABDE，连接AD、EC．若BD=CD，求证：四边形ADCE是矩形．
分析 已知四边形ABDE是平行四边形，只需证得它的一个内角是直角即可；在等腰△ABC中，AD是底边的中线，根据等腰三角形三线合一的性质即可证得∠ADC是直角，由此得证．
解答 证明：∵四边形ABDE是平行四边形
∴BD∥AE（即AE∥CD），BD=AE，
又∵BD=CD，
∴AE=CD，
∴四边形ADCE是平行四边形；
在△ABC中，AB=AC，BD=CD，
∴AD⊥BC，
∴∠ADC=90°，
∴?ADCE是矩形．
点评 此题主要考查了等腰三角形三线合一的性质以及矩形的判定方法，解题的关键是牢记矩形的三种判定方法，难度不大．
练习册系列答案
名校课堂系列答案
相关题目
6．下列说法中不正确的是（ ）
| A． | 抛掷一枚硬币，硬币落地时正面朝上是随机事件 | |
| B． | 把4个球放入三个抽屉中，其中一个抽屉中至少有2个球是必然事件 | |
| C． | 任意打开七年级下册数学教科书，正好是97页是确定事件 | |
| D． | 在相同条件下，只要试验的次数足够多，频率就可以作为概率的估计值 |
3．
如图，在Rt△ABC中，∠C=90°，∠A=30°，AC=2，则AB=（ ）
如图，在Rt△ABC中，∠C=90°，∠A=30°，AC=2，则AB=（ ）| A． | 4 | B． | $\frac{2\sqrt{3}}{3}$ | C． | $\frac{4\sqrt{3}}{3}$ | D． | $\frac{\sqrt{3}}{3}$ |
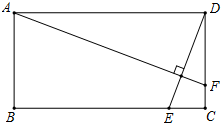如图，矩形ABCD中，AB=2，AD=4，动点E在边BC上，与点B、C不重合，过点A作DE的垂线，交直线CD于点F．设DF=x，EC=y．