题目内容
6.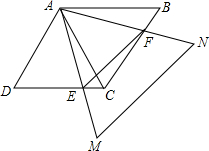 如图,△ABC、△ADC、△AMN均为等边三角形,AM>AB,AM与DC交于点E,AN与BC交于点F.
如图,△ABC、△ADC、△AMN均为等边三角形,AM>AB,AM与DC交于点E,AN与BC交于点F.(1)求证:△ABF≌△ACE;
(2)猜测△AEF的形状,并证明你的结论;
(3)请直接指出当F点在BC何处时,AC⊥EF.
分析 (1)由等边三角形的性质得出∠B=∠BAC=∠DAC=∠ACD=∠MAN=60°,AB=AC,可得∠BAF=∠CAE,由ASA证明△ABF≌△ACE即可;
(2)由全等三角形的性质得出AE=AF,得出△AEF是等边三角形即可;
(3)由等边三角形的性质得出∠CAF=$\frac{1}{2}$∠EAF=30°,由三角形的外角性质证出∠AFB=90°,求出∠BAF=30°,由含30°角的直角三角形的性质得出BF=$\frac{1}{2}$AB=$\frac{1}{2}$BC即可.
解答 (1)证明:∵△ABC、△ADC、△AMN均为等边三角形,
∴∠B=∠BAC=∠DAC=∠ACD=∠MAN=60°,AB=AC,
∴∠BAF=∠CAE,
在△ABF和△ACE中,
$\left\{\begin{array}{l}{∠B=∠ACD}&{\;}\\{AB=AC}&{\;}\\{∠BAF=∠CAE}&{\;}\end{array}\right.$,
∴△ABF≌△ACE(ASA);
(2)解:△AEF是等边三角形,理由如下:
由(1)得:△ABF≌△ACE,
∴AE=AF,
∵∠MAN=60°,
∴△AEF是等边三角形;
(3)解:当F在BC的中点时,AC⊥EF;理由如下:
∵△AEF是等边三角形,AC⊥EF,
∴∠CAF=$\frac{1}{2}$∠EAF=30°,
∴∠AFB=∠CAF+∠ACB=30°+60°=90°,∠BAF=60°-30°=30°,
∴BF=$\frac{1}{2}$AB=$\frac{1}{2}$BC,即F为BC的中点.
点评 本题考查了等边三角形的判定与性质、全等三角形的判定与性质、含30°角的直角三角形的性质等知识;熟练掌握等边三角形的判定与性质,证明三角形全等是解决问题的关键.

| A. | $\frac{3xy}{π}$ | B. | $\frac{5a-b}{2x-y}$ | C. | $\frac{{x}^{2}+1}{2}$ | D. | $\frac{x}{2}$-$\frac{1}{3}$ |
| A. | 3$\sqrt{2}$-$\sqrt{2}$=3 | B. | $\sqrt{14}$×$\sqrt{7}$=7$\sqrt{2}$ | C. | $\sqrt{60}$÷$\sqrt{5}$=2$\sqrt{3}$ | D. | $\sqrt{25a}$+$\sqrt{9a}$=8$\sqrt{a}$ |
| A. | b<a<c | B. | b<c<a | C. | c<b<a | D. | a<c<b |
| A. | a=2,b=1 | B. | a=2,b=-1 | C. | a=1,b=2 | D. | a=-2,b=-1 |
| A. | a-2=-$\frac{1}{{a}^{2}}$(a≠0) | B. | $\sqrt{(-2)^{2}}$=-2 | C. | a0=0(a≠0) | D. | $\root{3}{(-2)^{3}}$=-2 |
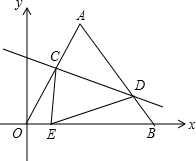 如图坐标系中,O(0,0),A(6,6$\sqrt{3}$),B(12,0),将△OAB沿直线线CD折叠,使点A恰好落在线段OB上的点E处,若OE=$\frac{24}{5}$,则CE:DE的值是$\frac{7}{8}$.
如图坐标系中,O(0,0),A(6,6$\sqrt{3}$),B(12,0),将△OAB沿直线线CD折叠,使点A恰好落在线段OB上的点E处,若OE=$\frac{24}{5}$,则CE:DE的值是$\frac{7}{8}$.