题目内容
1.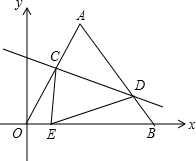 如图坐标系中,O(0,0),A(6,6$\sqrt{3}$),B(12,0),将△OAB沿直线线CD折叠,使点A恰好落在线段OB上的点E处,若OE=$\frac{24}{5}$,则CE:DE的值是$\frac{7}{8}$.
如图坐标系中,O(0,0),A(6,6$\sqrt{3}$),B(12,0),将△OAB沿直线线CD折叠,使点A恰好落在线段OB上的点E处,若OE=$\frac{24}{5}$,则CE:DE的值是$\frac{7}{8}$.
分析 过A作AF⊥OB于F,根据已知条件得到△AOB是等边三角形,推出△CEO∽△DBE,根据相似三角形的性质得到$\frac{OE}{BD}=\frac{CE}{ED}=\frac{CD}{EB}$,设CE=a,则CA=a,CO=12-a,ED=b,则AD=b,OB=12-b,于是得到24b=60a-5ab,36a=60b-5ab,两式相减得到36a-24b=60b-60a,即可得到结论.
解答  解:过A作AF⊥OB于F,
解:过A作AF⊥OB于F,
∵A(6,6$\sqrt{3}$),B(12,0),
∴AF=6$\sqrt{3}$,OF=6,OB=12,
∴BF=6,
∴OF=BF,
∴AO=AB,
∵tan∠AOB=$\frac{AF}{OF}=\sqrt{3}$,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴∠AOB=∠ABO=60°,
∵将△OAB沿直线线CD折叠,使点A恰好落在线段OB上的点E处,
∴∠CED=∠OAB=60°,
∴∠OCE=∠DEB,
∴△CEO∽△DBE,
∴$\frac{OE}{BD}=\frac{CE}{ED}=\frac{CD}{EB}$,
设CE=a,则CA=a,CO=12-a,ED=b,则AD=b,DB=12-b,
$\frac{\frac{24}{5}}{12-b}=\frac{a}{b}$,
∴24b=60a-5ab ①,
$\frac{12-a}{\frac{36}{5}}=\frac{a}{b}$,
∴36a=60b-5ab ②,
②-①得:36a-24b=60b-60a,
∴$\frac{a}{b}$=$\frac{7}{8}$,
即CE:DE=$\frac{7}{8}$.
故答案为:$\frac{7}{8}$.
点评 本题考查了翻折变换-折叠问题,相似三角形的判定和性质,等边三角形的判定和性质,证得△AOB是等边三角形是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | (b2)3 | B. | b3•b2 | C. | b10÷b2 | D. | (-b)5 |

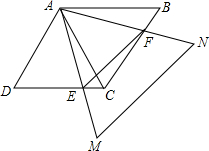 如图,△ABC、△ADC、△AMN均为等边三角形,AM>AB,AM与DC交于点E,AN与BC交于点F.
如图,△ABC、△ADC、△AMN均为等边三角形,AM>AB,AM与DC交于点E,AN与BC交于点F.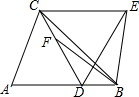 在△ABC中,∠A=60°,∠ABC=45°,点D是边AB上任意一点,连接CD.若∠BCD=15°,以线段CD为边在CD的有上方作正△CDE,连接BE,点F在线段CD上,且CF=BD,连接BF.求证:BE=BF.
在△ABC中,∠A=60°,∠ABC=45°,点D是边AB上任意一点,连接CD.若∠BCD=15°,以线段CD为边在CD的有上方作正△CDE,连接BE,点F在线段CD上,且CF=BD,连接BF.求证:BE=BF.