题目内容

4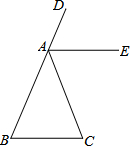．如图，BD为一直线，∠B=∠C，AE平分∠DAC，请说明AE∥BC．

分析 根据三角形的外角性质得出∠DAC=∠B+∠C，求出∠DAC=2∠B，根据角平分线定义得出∠DAC=2∠DAE，求出∠DAE=∠B，根据平行线的判定得出即可．

解答 证明：∵∠DAC是△ABC的外角，
∴∠DAC=∠B+∠C，
∵∠B=∠C，
∴∠DAC=2∠B，
∵AE平分∠DAC，
∴∠DAC=2∠DAE，
∴∠DAE=∠B，
∴AE∥BC．

点评 本题考查了三角形的外角性质和平行线的判定的应用，能求出∠DAE=∠B是解此题的关键．

练习册系列答案
相关题目
12．在Rt△AOB中，OA=3，sinB=$\frac{3}{5}$，P、M、分别是BA、BO边上的两个动点．点M从点B出发，沿BO以1单位/秒的速度向点O运动；点P从点B出发，沿BA以a单位/秒的速度向点A运动；P、M两点同时出发，任意一点先到达终点时，两点停止运动．设运动的时间为t．
（1）线段AP的长度为5-at（用含a、t的代数式表示）；
（2）如图①，连结PO、PM，若a=1，△PMO的面积为S，试求S的最大值；
（3）如图②，连结PM、AM，试探究：在点P、M运动的过程中，是否存在某个时刻，使得△PMB为直角三角形且△PMA是等腰三角形？若存在，求出此时a和t的取值，若不存在，请说明理由．
15．如图，在△ABC中，AB=AC=13厘米，BC=10厘米．AD⊥BC于点D，动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动，设动点运动的时间为t秒．
（1）求AD的长；
（2）当△PDC的面积为15平方厘米时，求t的值；
（3）动点M从点C出发以每秒2厘米的速度在射线CB上运动．点M与点P同时出发，且当点P运动到终点D时，点M也停止运动．是否存在t，使得PM=AP+BM？若存在，请求出t的值；若不存在，请说明理由．
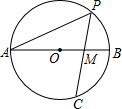12．如图，在⊙O中，AB为直径，PC为弦，且PA=PC，PC交AB于M，若∠APC=45°，求$\frac{AM}{BM}$的值．
19．分解因式：
（1）6x（a-b）+4y（b-a）
（2）9（a+b）2-25（a-b）2．
9．如图，△ABC是等边三角形，AB=2，D是边BC的中点，点P从点A出发，沿AB-BD以每秒1个单位长度的速度向终点D运动．同时点Q从点C出发，沿CA-AC以每秒1个单位长度的速度运动．当点P停止运动时，点Q也随之停止运动，设点P的运动时间为t（秒），△PQD的面积为S．
（1）求线段PB的长（用含t的代数式）．
（2）当△PQD是等边三角形时，求t的值．
（3）当S＞0时，求S与t的函数关系式．
（4）若点D关于直线PQ的对称点为点D′，且S＞0，直接写出点D′落在△ABC的边上时t的值．
16．如图，在一张矩形纸片ABCD中，AB=4，BC=8，点E，F分别在AD，BC上，将纸片ABCD沿直线EF折叠，点C落在AD上的一点H处，点D落在点G处，有以下四个结论：
①四边形CFHE是菱形；
②EC平分∠DCH；
③线段BF的取值范围为3≤BF≤4；
④当点H与点A重合时，EF=2$\sqrt{5}$．
以上结论中，你认为正确的有①③④．（填序号）
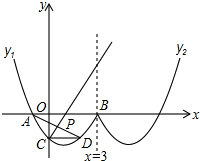13．如图形似“w”的函数是由抛物线y1的一部分，其表达式为：y1=$\frac{\sqrt{3}}{3}$（x2-2x-3）（x≤3）以及抛物线y2的一部分所构成的，其中曲线y2与曲线y1关于直线x=3对称，A、B是曲线y1与x轴两交点（A在B的左边），C是曲线y1与y轴交点．
（1）求A，B，C三点的坐标和曲线y2的表达式；
（2）我们把其中一条对角线被另一条对角线垂直且平分的四边形称为筝形．过点C作x轴的平行线与曲线y1交于另一个点D，连接AD．试问：在曲线y2上是否存在一点M，使得四边形ACDM为筝形？若存在，计算出点M的横坐标，若不存在，说明理由．
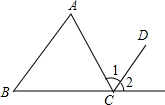14．已知：如图，AB∥CD，若∠A=66°∠B=45°，则∠1=66°，∠2=45°．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网