题目内容
16. 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2$\sqrt{5}$.
以上结论中,你认为正确的有①③④.(填序号)
分析 ①先判断出四边形CFHE是平行四边形,再根据翻折的性质可得CF=FH,然后根据邻边相等的平行四边形是菱形证明,判断出①正确;
②根据菱形的对角线平分一组对角线可得∠BCH=∠ECH,然后求出只有∠DCE=30°时EC平分∠DCH,判断出②错误;
③点H与点A重合时,设BF=x,表示出AF=FC=8-x,利用勾股定理列出方程求解得到BF的最小值,点G与点D重合时,CF=CD,求出BF=4,然后写出BF的取值范围,判断出③正确;
④过点F作FM⊥AD于M,求出ME,再利用勾股定理列式求解得到EF,判断出④正确.
解答 解:∵FH与CG,EH与CF都是矩形ABCD的对边AD、BC的一部分,
∴FH∥CG,EH∥CF,
∴四边形CFHE是平行四边形,
由翻折的性质得,CF=FH,
∴四边形CFHE是菱形,(故①正确);
∴∠BCH=∠ECH,
∴只有∠DCE=30°时EC平分∠DCH,(故②错误);
点H与点A重合时,设BF=x,则AF=FC=8-x,
在Rt△ABF中,AB2+BF2=AF2,
即42+x2=(8-x)2,
解得x=3,
点G与点D重合时,CF=CD=4,
∴BF=4,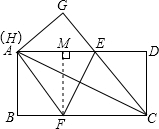 ∴线段BF的取值范围为3≤BF≤4,(故③正确);
∴线段BF的取值范围为3≤BF≤4,(故③正确);
过点F作FM⊥AD于M,
则ME=(8-3)-3=2,
由勾股定理得,
EF=$\sqrt{M{F}^{2}+M{E}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,(故④正确);
综上所述,结论正确的有①③④共3个,
故答案为①③④.
点评 本题考查了翻折变换的性质,菱形的判定与性质,勾股定理的应用,难点在于灵活运用菱形的判定与性质与勾股定理等其它知识有机结合.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
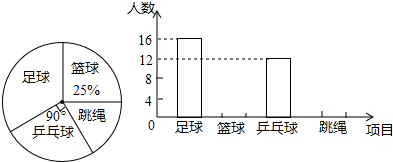
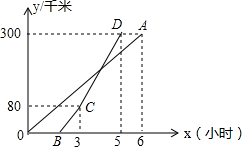 甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地如图、线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系,根据图象解答下列问题:
甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地如图、线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系,根据图象解答下列问题: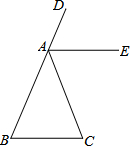 如图,BD为一直线,∠B=∠C,AE平分∠DAC,请说明AE∥BC.
如图,BD为一直线,∠B=∠C,AE平分∠DAC,请说明AE∥BC.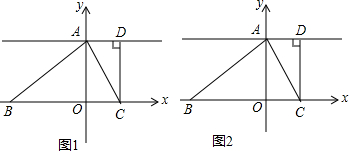
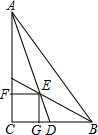 如图,在Rt△ABC中,∠C=90°,∠BAC=40°,AD是△ABC的一条角平分线,点E,F,G分别在AD,AC,BC上,且四边形CGEF是正方形,则∠DEB的度数为( )
如图,在Rt△ABC中,∠C=90°,∠BAC=40°,AD是△ABC的一条角平分线,点E,F,G分别在AD,AC,BC上,且四边形CGEF是正方形,则∠DEB的度数为( )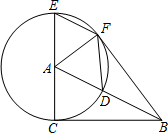 如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.
如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.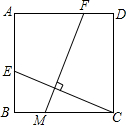 已知:如图,正方形ABCD中,点E、M、F分别在AB、BC、AD上,如果CE⊥FM,求证:CE=FM.
已知:如图,正方形ABCD中,点E、M、F分别在AB、BC、AD上,如果CE⊥FM,求证:CE=FM.