题目内容
12.在Rt△AOB中,OA=3,sinB=$\frac{3}{5}$,P、M、分别是BA、BO边上的两个动点.点M从点B出发,沿BO以1单位/秒的速度向点O运动;点P从点B出发,沿BA以a单位/秒的速度向点A运动;P、M两点同时出发,任意一点先到达终点时,两点停止运动.设运动的时间为t.(1)线段AP的长度为5-at(用含a、t的代数式表示);
(2)如图①,连结PO、PM,若a=1,△PMO的面积为S,试求S的最大值;
(3)如图②,连结PM、AM,试探究:在点P、M运动的过程中,是否存在某个时刻,使得△PMB为直角三角形且△PMA是等腰三角形?若存在,求出此时a和t的取值,若不存在,请说明理由.

分析 (1)根据三角函数得出AB的长度解答即可;
(2)过点P作PD⊥OB,根据三角形的面积公式和二次函数的最值解答即可;
(3)根据直角三角形的性质和等腰三角形的性质进行解答即可.
解答 解:(1)∵Rt△AOB中,OA=3,sinB=$\frac{3}{5}$,
∴AB=5,
∵设运动的时间为t,点P从点B出发,沿BA以a单位/秒的速度向点A运动,
∴AP=5-at,
故答案为:5-at;
(2)如图①: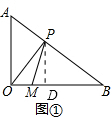
过点P作PD⊥OB,在Rt△PDB中,PB=t,sinB=$\frac{3}{5}$,
∴PD=$\frac{3}{5}t$,OM=4-t,
∴$S=\frac{1}{2}(4-t)•\frac{3}{5}t=-\frac{3}{10}(t-2)^{2}+\frac{6}{5}$,
∵0≤t≤4,
∴当t=2时,${S}_{最大值}=\frac{6}{5}$;
(3)假设存在,
①若∠PMB=90°,如图②: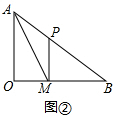
∵PA=PM,
在Rt△PMB中,PB=at,sinB=$\frac{3}{5}$,
∴PM=$\frac{3}{5}$at,MB=$\frac{4}{5}$at,
根据题意可得:$\left\{\begin{array}{l}{5-at=\frac{3}{5}at}\\{\frac{4}{5}at=t}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{5}{4}}\\{t=\frac{5}{2}}\end{array}\right.$,符合题意;
②若∠MPB=90°,如图③,则∠APM=90°,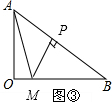
∴PA=PM,
在Rt△PMB中,PB=at,sinB=$\frac{3}{5}$,
∴$PM=\frac{3}{4}at,MB=\frac{5}{4}at$,
根据题意可得:$\left\{\begin{array}{l}{5-at=\frac{3}{4}at}\\{\frac{5}{4}at=t}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{4}{5}}\\{t=\frac{25}{7}}\end{array}\right.$,符合题意,
∴存在某时刻,使得△PMB为直角三角形且△PMA是等腰三角形,此时$\left\{\begin{array}{l}{{a}_{1}=\frac{5}{4}}\\{{t}_{1}=\frac{5}{2}}\end{array}\right.或\left\{\begin{array}{l}{{a}_{2}=\frac{4}{5}}\\{{t}_{2}=\frac{25}{7}}\end{array}\right.$.
点评 此题主要考查了三角形综合题,关键是根据三角函数得出AB的长度,同时根据直角三角形的性质和等腰三角形的性质解答.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案| A. | (4,1) | B. | (5,1) | C. | (6,1) | D. | (7,1) |
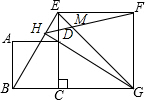 如图,正方形ABCD的顶点D在正方形ECGF的边EC上,顶点B在GC的延长线上,连接EG、BE,∠EGC的平分线GH过点D交BE于H,连接HF交EG于M,则$\frac{MG}{ME}$的值为$\sqrt{2}$+1.
如图,正方形ABCD的顶点D在正方形ECGF的边EC上,顶点B在GC的延长线上,连接EG、BE,∠EGC的平分线GH过点D交BE于H,连接HF交EG于M,则$\frac{MG}{ME}$的值为$\sqrt{2}$+1.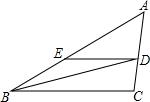 如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=50°,∠BDC=75°.求∠BED的度数.
如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=50°,∠BDC=75°.求∠BED的度数.

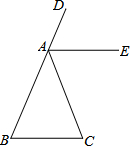 如图,BD为一直线,∠B=∠C,AE平分∠DAC,请说明AE∥BC.
如图,BD为一直线,∠B=∠C,AE平分∠DAC,请说明AE∥BC.