题目内容
14.阅读1:a、b为实数,且a>0,b>0因为($\sqrt{a}$-$\sqrt{b}$)2≥0,所以a-2$\sqrt{ab}$+b≥0从而a+b≥2$\sqrt{ab}$(当a=b时取等号).阅读2:若函数y=x+$\frac{m}{x}$;(m>0,x>0,m为常数),由阅读1结论可知:x+$\frac{m}{x}$≥2$\sqrt{m}$,所以当x=$\frac{m}{x}$,即x=$\sqrt{m}$时,函数y=x+$\frac{m}{x}$的最小值为2$\sqrt{m}$.
阅读理解上述内容,解答下列问题:
问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为$\frac{4}{x}$,周长为2(x+$\frac{4}{x}$),求当x=2时,周长的最小值为8;
问题2:已知函数y1=x+1(x>-1)与函数y2=x2+2x+10(x>-1),当x=2时,$\frac{{y}_{2}}{{y}_{1}}$的最小值为6.
分析 问题1:根据阅读1、2给定内容可知:当x=$\frac{4}{x}$,x+$\frac{4}{x}$有最小值,解方程求出x的值,代入x+$\frac{m}{x}$≥2$\sqrt{m}$即可得出结论;
问题2:根据给定y1、y2找出$\frac{{y}_{2}}{{y}_{1}}$=(x+1)+$\frac{9}{x+1}$,由阅读材料可知当x+1=$\frac{9}{x+1}$时,$\frac{{y}_{2}}{{y}_{1}}$有最小值,解方程求出x的值,再代入x+$\frac{m}{x}$≥2$\sqrt{m}$即可得出结论.
解答 解:问题1:∵矩形的一边长为x,另一边长为$\frac{4}{x}$,
∴x>0.
令x=$\frac{4}{x}$,解得:x=2,
∴x=2时,x+$\frac{4}{x}$有最小值为2×$\sqrt{x•\frac{4}{x}}$=4,
∴当x=2时,周长的最小值为2×4=8.
故答案为:2;8.
问题2:∵函数y1=x+1(x>-1),函数y2=x2+2x+10(x>-1),
∴$\frac{{y}_{2}}{{y}_{1}}$=$\frac{{x}^{2}+2x+10}{x+1}$=(x+1)+$\frac{9}{x+1}$,
∵x>-1,
∴x+1>0.
令x+1=$\frac{9}{x+1}$,解得:x=2,或x=-4(舍去),
∴当x=2时,(x+1)+$\frac{9}{x+1}$有最小值为2×$\sqrt{(x+1)•\frac{9}{x+1}}$=6.
点评 本题考查了反比例的综合应用,解题的关键是根据阅读材料的结论“x+$\frac{m}{x}$≥2$\sqrt{m}$,所以当x=$\frac{m}{x}$,即x=$\sqrt{m}$时,函数y=x+$\frac{m}{x}$的最小值为2$\sqrt{m}$”解决问题.本题属于中档题,难度不大,解决该题型题目时,根据阅读材料给出的结论解决问题是关键.

 阅读快车系列答案
阅读快车系列答案 同一直角坐标系中,一次函数y1=k1x+b与正比例函数y2=k2x的图象如图所示,则当y1大于y2时,x取值范围是( )
同一直角坐标系中,一次函数y1=k1x+b与正比例函数y2=k2x的图象如图所示,则当y1大于y2时,x取值范围是( )| A. | x>0 | B. | x<0 | C. | x<-2 | D. | x>-2 |
| A. | 折线图 | B. | 条形图 | C. | 扇形图 | D. | 直方图 |
 如图,直线AB、CD相交于点O,OD平分∠BOF,OE⊥CD于O,若∠EOF=α,下列说法①∠AOC=α-90°;②∠EOB=180°-α;③∠AOF=360°-2α,其中正确的是( )
如图,直线AB、CD相交于点O,OD平分∠BOF,OE⊥CD于O,若∠EOF=α,下列说法①∠AOC=α-90°;②∠EOB=180°-α;③∠AOF=360°-2α,其中正确的是( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
| A. | 3 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{3}$或$\sqrt{5}$ |
 如图,一块正方形,边长是18cm,上面横竖各有两道黑条(阴影部分),宽度都是2cm,请利用平移的知识求出图中白色部分的面积.
如图,一块正方形,边长是18cm,上面横竖各有两道黑条(阴影部分),宽度都是2cm,请利用平移的知识求出图中白色部分的面积.
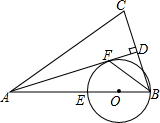 如图,在△ABC中,AB=AC,AD是BC边上的高线,BF平分∠ABC交AD于点F,以AB上的点O为圆心,OB为半径的⊙O交AB于点E,恰好经过点F.
如图,在△ABC中,AB=AC,AD是BC边上的高线,BF平分∠ABC交AD于点F,以AB上的点O为圆心,OB为半径的⊙O交AB于点E,恰好经过点F.