题目内容
4.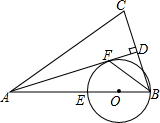 如图,在△ABC中,AB=AC,AD是BC边上的高线,BF平分∠ABC交AD于点F,以AB上的点O为圆心,OB为半径的⊙O交AB于点E,恰好经过点F.
如图,在△ABC中,AB=AC,AD是BC边上的高线,BF平分∠ABC交AD于点F,以AB上的点O为圆心,OB为半径的⊙O交AB于点E,恰好经过点F.(1)求证:AD与⊙O相切;
(2)当BC=4,AC=6时,求线段AE的长.
分析 (1)连接OF,由AB=AC可得出∠OBF=∠OFB,由BF平分∠ABC可得出∠OBF=∠DBF,根据等量替换可得出∠DBF=∠OFB,进而得出OF∥BD,再结合AD是BC边上的高线即可得出OF⊥AD,此题得证;
(2)由AB=AC,AD是BC边上的高线,即可得出BD、AB的长度,根据OF∥BD即可得出△AOF∽△ABD,根据相似三角形的性质可得出$\frac{OF}{BD}=\frac{AO}{AB}$,进而求出OF的长度,此题得解.
解答 解:(1)证明:连接OF,如图所示.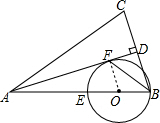
∵OB=OF,
∴∠OBF=∠OFB.
∵BF平分∠ABC,
∴∠OBF=∠DBF,
∴∠DBF=∠OFB,
∴OF∥BD.
∵AD是BC边上的高线,
∴OF⊥AD,
∴AD与⊙O相切.
(2)∵AB=AC,AD是BC边上的高线,
∴BD=$\frac{1}{2}$BC=2.
∵AC=6,
∴AB=6,
∵OF∥BD,
∴△AOF∽△ABD,
∴$\frac{OF}{BD}=\frac{AO}{AB}$.
设半径为r,得:$\frac{r}{2}=\frac{6-r}{6}$,
解得:r=$\frac{3}{2}$,
∴AE=3.
点评 本题考查了等腰三角形的性质、切线的判定以及相似三角形的判定与性质,解题的关键是:(1)找出OF∥BD;(2)根据相似三角形的性质得出$\frac{OF}{BD}=\frac{AO}{AB}$.本题属于中档题,难度不大,解决该题型题目时,利用平行线的性质(全等三角形或相似三角形)找出垂直关系是关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
12.下列各语句中,正确的是( )
| A. | 两条直线被第三条直线所截,同位角相等 | |
| B. | 若a⊥b,c⊥b,则a⊥c | |
| C. | 若a∥b,c∥d,则a∥d | |
| D. | 同旁内角互补,两直线平行 |
13. 已知:如图,将∠ABC放置在正方形网格纸中,其中点A、B、C均在格点上,则tan∠ABC的值是( )
已知:如图,将∠ABC放置在正方形网格纸中,其中点A、B、C均在格点上,则tan∠ABC的值是( )
 已知:如图,将∠ABC放置在正方形网格纸中,其中点A、B、C均在格点上,则tan∠ABC的值是( )
已知:如图,将∠ABC放置在正方形网格纸中,其中点A、B、C均在格点上,则tan∠ABC的值是( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
 如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为1或5.
如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为1或5.
 如图所示,在平面直角坐标系中,“鱼”的每个“顶点”都在小正方形的顶点处,点A为“鱼”的一个顶点,将“鱼”向右平移3个单位长度,再向下平移6个单位长度,则平移后点A的坐标为(-1,0).
如图所示,在平面直角坐标系中,“鱼”的每个“顶点”都在小正方形的顶点处,点A为“鱼”的一个顶点,将“鱼”向右平移3个单位长度,再向下平移6个单位长度,则平移后点A的坐标为(-1,0). 有理数a、b在数轴上的对应的位置如图所示,则下列各式①a+b<0;②a-b>0;③ab>0;④|a|>b;⑤1-b>0;⑥a+1<0,一定成立的有( )
有理数a、b在数轴上的对应的位置如图所示,则下列各式①a+b<0;②a-b>0;③ab>0;④|a|>b;⑤1-b>0;⑥a+1<0,一定成立的有( ) 如图,在平面直角坐标系中,已知A(0,2),M(6,4),N(8,8),动点P从点A出发,沿y轴以每秒2个单位长度的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
如图,在平面直角坐标系中,已知A(0,2),M(6,4),N(8,8),动点P从点A出发,沿y轴以每秒2个单位长度的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.