题目内容
7．设S=2x2+2xy+y2+2x+1，其中x，y为实数，则S的最小值为（ ）| A． | -1 | B． | 1 | C． | $-\frac{3}{4}$ | D． | 0 |
分析 首先将S=2x2+2xy+y2+2x+1式子通过拆分项、完全平方式转化为S=（x+y）2+（x+1）2-1．再根据非负数的性质，即可得解．
解答 解：∵S=2x2+2xy+y2+2x+1=（x+y）2+（x+1）2-1，
∴S的最小值为-1．
故选：A．
点评 此题考查了配方法的应用，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
15．若关于x的方程$\frac{2}{x-3}$=1-$\frac{m}{x-3}$无解，则m的值是（ ）
| A． | 3 | B． | 2 | C． | -3 | D． | -2 |
12．计算2a2-（a-3）2，正确的结果是（ ）
| A． | 6a-9 | B． | 6a+9 | C． | a2+6a+9 | D． | a2+6a-9 |
19．
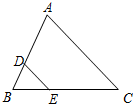如图，△ABC中，若DE∥AC，则下列等式不成立的是（ ）
如图，△ABC中，若DE∥AC，则下列等式不成立的是（ ）| A． | $\frac{AD}{BD}=\frac{CE}{EB}$ | B． | $\frac{AD}{AB}=\frac{CE}{CB}$ | C． | $\frac{BD}{BA}=\frac{BE}{BC}$ | D． | $\frac{DE}{AC}=\frac{BE}{EC}$ |
如图，抛物线y=-$\frac{5}{4}$x2+bx+c与y轴交于点A（0，1），过点A的直线与抛物线交于另一点B（3，$\frac{5}{2}$），过点B作BC⊥x轴，垂足为C．
一大门的栏杆如图所示，BA⊥AE，若CD∥AE，则∠ABC+∠BCD=270度．