题目内容
2.计算:(1)(-a3)2•(a2)3
(2)4-(-2)-2-32÷(3.14-π)0.
分析 (1)先算幂的乘方,再算同底数幂的乘法;
(2)先算负整数指数幂,零指数幂,平方,再计算除法,最后计算加减法即可求解.
解答 解:(1)(-a3)2•(a2)3
=a6•a6
=a12;
(2)4-(-2)-2-32÷(3.14-π)0
=4-$\frac{1}{4}$-9÷1
=4-$\frac{1}{4}$-9
=-5$\frac{1}{4}$.
点评 此题考查了整式的混合运算,它们分别利用了幂的乘方,同底数幂的乘法等知识.容易混淆,一定要记准法则才能做题.同时考查了实数的运算.

练习册系列答案
相关题目
4.下列变形不是根据等式性质的是( )
| A. | $\frac{0.3x}{0.5y}$=$\frac{3x}{5y}$ | B. | 若-a=x,则x+a=0 | ||
| C. | 若x-3=2-2x,则x+2x=2+3 | D. | 若-$\frac{1}{2}$x=1,则x=-2 |
5.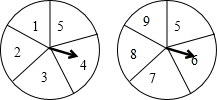 如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是( )
如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是( )
 如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是( )
如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是( )| A. | $\frac{2}{25}$ | B. | $\frac{4}{25}$ | C. | $\frac{6}{25}$ | D. | $\frac{9}{25}$ |
7.设S=2x2+2xy+y2+2x+1,其中x,y为实数,则S的最小值为( )
| A. | -1 | B. | 1 | C. | $-\frac{3}{4}$ | D. | 0 |
14.已知x2-y2=4,x-y=2,则x+y等于( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
12.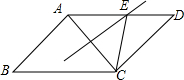 如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )
如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )
 如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )
如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )| A. | 6 | B. | 8 | C. | 14 | D. | 16 |