题目内容
10.解不等式组$\left\{\begin{array}{l}{1-2(x-1)>1}\\{\frac{x}{2}-\frac{1}{3}≥x}\end{array}\right.$,并把其解集在数轴上表示出来.分析 分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:解不等式1-2(x-1)>1,得:x<1,
解不等式$\frac{x}{2}-\frac{1}{3}$≥x,得:x≤-$\frac{2}{3}$,
故不等式组的解集为:x$≤-\frac{2}{3}$,
将不等式组解集表示在数轴上如下: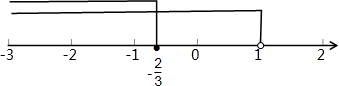
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20. 如图,在⊙O中,O为圆心,点A,B,C在圆上,若OA=AB,则∠ACB=( )
如图,在⊙O中,O为圆心,点A,B,C在圆上,若OA=AB,则∠ACB=( )
 如图,在⊙O中,O为圆心,点A,B,C在圆上,若OA=AB,则∠ACB=( )
如图,在⊙O中,O为圆心,点A,B,C在圆上,若OA=AB,则∠ACB=( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
1.某班一个小组7名同学的体育测试成绩(满分30分)依次为:27,29,27,25,27,30,25,这组数据的中位数和众数分别是( )
| A. | 27,25 | B. | 25,27 | C. | 27,27 | D. | 27,30 |
18.|-2|=x,则x的值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | $\sqrt{2}$ |
5.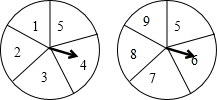 如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是( )
如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是( )
 如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是( )
如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是( )| A. | $\frac{2}{25}$ | B. | $\frac{4}{25}$ | C. | $\frac{6}{25}$ | D. | $\frac{9}{25}$ |
7.设S=2x2+2xy+y2+2x+1,其中x,y为实数,则S的最小值为( )
| A. | -1 | B. | 1 | C. | $-\frac{3}{4}$ | D. | 0 |
 如图,已知点D为CB的中点,∠B=45°,CE⊥AD,AC⊥CB,连接DE,求证:CE+DE=AD.
如图,已知点D为CB的中点,∠B=45°,CE⊥AD,AC⊥CB,连接DE,求证:CE+DE=AD.