题目内容
9.若关于x的一元二次方程x2+x-a+$\frac{9}{4}$=0有两个不相等的实数根,则实数a的取值范围是a>2.分析 关于x的一元二次方程x2+x-a+$\frac{9}{4}$=0有两个不相等的实数根,方程必须满足△=b2-4ac>0,即可求得.
解答 解:∵关于x的一元二次方程x2+x-a+$\frac{9}{4}$=0有两个不相等的实数根,
∴△=b2-4ac=1+4a-9>0,
解得a>2.
故答案为:a>2.
点评 本题考查了一元二次方程根的判别式一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
20. 如图,在⊙O中,O为圆心,点A,B,C在圆上,若OA=AB,则∠ACB=( )
如图,在⊙O中,O为圆心,点A,B,C在圆上,若OA=AB,则∠ACB=( )
 如图,在⊙O中,O为圆心,点A,B,C在圆上,若OA=AB,则∠ACB=( )
如图,在⊙O中,O为圆心,点A,B,C在圆上,若OA=AB,则∠ACB=( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
17.下列运算正确的是( )
| A. | 3a3+4a3=7a6 | B. | 3a2•a2=4a2 | C. | (a+2)2=a2+4 | D. | (-a4)2=a8 |
4.下列变形不是根据等式性质的是( )
| A. | $\frac{0.3x}{0.5y}$=$\frac{3x}{5y}$ | B. | 若-a=x,则x+a=0 | ||
| C. | 若x-3=2-2x,则x+2x=2+3 | D. | 若-$\frac{1}{2}$x=1,则x=-2 |
14.在已知实数:-1,0,$\sqrt{2}$,-2中,最大的一个实数是( )
| A. | -1 | B. | 0 | C. | $\sqrt{2}$ | D. | -2 |
1.某班一个小组7名同学的体育测试成绩(满分30分)依次为:27,29,27,25,27,30,25,这组数据的中位数和众数分别是( )
| A. | 27,25 | B. | 25,27 | C. | 27,27 | D. | 27,30 |
18.|-2|=x,则x的值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | $\sqrt{2}$ |
7.设S=2x2+2xy+y2+2x+1,其中x,y为实数,则S的最小值为( )
| A. | -1 | B. | 1 | C. | $-\frac{3}{4}$ | D. | 0 |
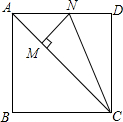 如图,已知正方形ABCD中,CM=CD,MN⊥AC,连接CN,则∠MNC=67.5°.
如图,已知正方形ABCD中,CM=CD,MN⊥AC,连接CN,则∠MNC=67.5°.