题目内容
19. 如图,等边三角形OAB的边长为2,P是线段OA上任意一点(不含端点O,A),过O、P两点的抛物线和过A,P两点的抛物线的顶点分别在OB,AB上,则这两个二次函数的最大值之和等于$\sqrt{3}$.
如图,等边三角形OAB的边长为2,P是线段OA上任意一点(不含端点O,A),过O、P两点的抛物线和过A,P两点的抛物线的顶点分别在OB,AB上,则这两个二次函数的最大值之和等于$\sqrt{3}$.
分析 连接PM、PN,根据二次函数的对称性可知OM=PM,PN=AN,从而判断出△POM和△ANP是等边三角形,再根据等边三角形的性质求解即可.
解答 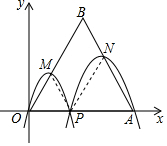 解:如图,连接PM、PN,
解:如图,连接PM、PN,
由二次函数的性质,OM=PM,PN=AN,
∵△OAB是等边三角形,
∴∠AOB=∠OAB=60°,
∴△POM和△ANP是等边三角形,
∵OA=2,
∴点B、C的纵坐标之和为2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
即两个二次函数的最大值之和等于$\sqrt{3}$.
故答案为$\sqrt{3}$.
点评 本题考查了二次函数的最值问题,等边三角形的判定与性质,作辅助线构造出等边三角形并利用等边三角形的知识求解是解题的关键.

练习册系列答案
相关题目
10.下列计算正确的是( )
| A. | 3a2+2a2=5a4 | B. | a•a=a2 | C. | 4a6÷2a2=2a3 | D. | 2a-a=2 |
4.下列方程,不适宜用因式分解法求解的是( )
| A. | x2=3x | B. | (x-2)2=3x-6 | C. | 4x2+4x+1=0 | D. | (x+2)(2x-1)=5 |
1.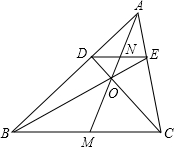 如图,△ABC中,DE∥BC,BE与CD交于点O,AO与DE、BC交于N、M,则下列式子中错误的是( )
如图,△ABC中,DE∥BC,BE与CD交于点O,AO与DE、BC交于N、M,则下列式子中错误的是( )
 如图,△ABC中,DE∥BC,BE与CD交于点O,AO与DE、BC交于N、M,则下列式子中错误的是( )
如图,△ABC中,DE∥BC,BE与CD交于点O,AO与DE、BC交于N、M,则下列式子中错误的是( )| A. | $\frac{DN}{BM}$=$\frac{AD}{AB}$ | B. | $\frac{AD}{AB}$=$\frac{DE}{BC}$ | C. | $\frac{DO}{OC}$=$\frac{DE}{BC}$ | D. | $\frac{AE}{EC}$=$\frac{AO}{OM}$ |
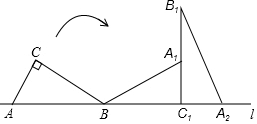 如图,Rt△ABC的斜边AB在直线l上,AC=1,AB=2.将Rt△ABC绕点B在平面内按顺时针方向旋转,使边BC落在直线l上,得到△A1BC1,再将△A1BC1绕点C1在平面内按顺时针方向旋转,使边A1C1落到直线l上,得到△A2B1C1,则点A所经过的两条弧的长度和为$\frac{13}{6}$π.
如图,Rt△ABC的斜边AB在直线l上,AC=1,AB=2.将Rt△ABC绕点B在平面内按顺时针方向旋转,使边BC落在直线l上,得到△A1BC1,再将△A1BC1绕点C1在平面内按顺时针方向旋转,使边A1C1落到直线l上,得到△A2B1C1,则点A所经过的两条弧的长度和为$\frac{13}{6}$π.
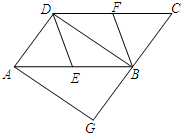 如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G,∠G=90°.
如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G,∠G=90°.