题目内容
1.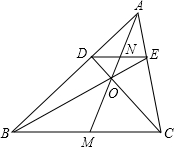 如图,△ABC中,DE∥BC,BE与CD交于点O,AO与DE、BC交于N、M,则下列式子中错误的是( )
如图,△ABC中,DE∥BC,BE与CD交于点O,AO与DE、BC交于N、M,则下列式子中错误的是( )| A. | $\frac{DN}{BM}$=$\frac{AD}{AB}$ | B. | $\frac{AD}{AB}$=$\frac{DE}{BC}$ | C. | $\frac{DO}{OC}$=$\frac{DE}{BC}$ | D. | $\frac{AE}{EC}$=$\frac{AO}{OM}$ |
分析 由DE∥BC,可得三角形相似,再根据相似三角形对应边成比例即可求解.
解答 解:∵DE∥BC,
∴△ADN∽△ABM,△ADE∽△ABC,△DOE∽△COB,
∴$\frac{DN}{BM}$=$\frac{AD}{AB}$,$\frac{AD}{AB}$=$\frac{DE}{BC}$,$\frac{DO}{OC}$=$\frac{DE}{BC}$,
所以A、B、C正确;
∵DE∥BC,
∴△AEN∽△ACM,
∴$\frac{AE}{AC}$=$\frac{AN}{AM}$,
∴$\frac{AE}{EC}$=$\frac{AN}{NM}$,
所以D错误.
故选D.
点评 本题考查了相似三角形的判定与性质.注意平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;相似三角形对应边成比例.注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20. 如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么BF:CF等于( )
如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么BF:CF等于( )
 如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么BF:CF等于( )
如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么BF:CF等于( )| A. | 5:8 | B. | 3:8 | C. | 3:5 | D. | 2:5 |
16.二次函数y=(x-m)2-m2-1有最小值-4,则实数m的值可能是( )
| A. | -$\sqrt{3}$ | B. | -3 | C. | $\sqrt{5}$ | D. | 4 |
 如图,等边三角形OAB的边长为2,P是线段OA上任意一点(不含端点O,A),过O、P两点的抛物线和过A,P两点的抛物线的顶点分别在OB,AB上,则这两个二次函数的最大值之和等于$\sqrt{3}$.
如图,等边三角形OAB的边长为2,P是线段OA上任意一点(不含端点O,A),过O、P两点的抛物线和过A,P两点的抛物线的顶点分别在OB,AB上,则这两个二次函数的最大值之和等于$\sqrt{3}$. 用5个完全相同的小正方体组成如图所示的立体图形,将右上角的小正方体拿掉后俯视图为( )
用5个完全相同的小正方体组成如图所示的立体图形,将右上角的小正方体拿掉后俯视图为( )



 如图,线段AB=2n,点P是线段AD上的动点(不包括端点),分别以AP.BP为斜边,在线段AB两侧作等腰Rt△ACP和等腰Rt△BDP,则C、D两点之间的距离为$\sqrt{2}$n.(用含n的代数式表示)
如图,线段AB=2n,点P是线段AD上的动点(不包括端点),分别以AP.BP为斜边,在线段AB两侧作等腰Rt△ACP和等腰Rt△BDP,则C、D两点之间的距离为$\sqrt{2}$n.(用含n的代数式表示)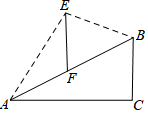 如图,小明家附近有一斜坡AB=40米,其坡度$i=1:\sqrt{3}$,斜坡AB上有一竖直向上的古树EF,小明在山底A处看古树树顶E的仰角为60°,在山顶B处看古树树顶E的仰角为15°,则古树的高约为(参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)( )
如图,小明家附近有一斜坡AB=40米,其坡度$i=1:\sqrt{3}$,斜坡AB上有一竖直向上的古树EF,小明在山底A处看古树树顶E的仰角为60°,在山顶B处看古树树顶E的仰角为15°,则古树的高约为(参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)( )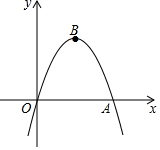 如图,在平面直角坐标系中,抛物线y=-x2+bx与x轴正半轴交于点A,顶点为B,当存在以AB为边,以点O为对称中心的矩形时,b的值为2$\sqrt{3}$.
如图,在平面直角坐标系中,抛物线y=-x2+bx与x轴正半轴交于点A,顶点为B,当存在以AB为边,以点O为对称中心的矩形时,b的值为2$\sqrt{3}$.