题目内容
8.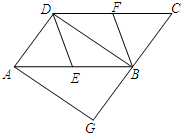 如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G,∠G=90°.
如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G,∠G=90°.(1)求证:四边形BEDF是菱形;
(2)当CD=CG时,请直接写出图中所有与∠C互补的角.
分析 (1)根据已知条件证明BE=DF,BE∥DF,从而得出四边形DFBE是平行四边形,再证明DE=BE,根据邻边相等的平行四边形是菱形,从而得出结论.
(2)先得到△BCF是等边三角形,即可得到图中所有与∠C互补的角.
解答 解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵点E、F分别是AB、CD的中点,
∴BE=$\frac{1}{2}$AB,DF=$\frac{1}{2}$CD,
∴BE=DF,BE∥DF,
∴四边形DFBE是平行四边形,
∵∠G=90°,AG∥BD,AD∥BG,
∴四边形AGBD是矩形,
∴∠ADB=90°,
∵在Rt△ADB中,E为AB的中点,
∴AE=BE=DE,
∴四边形DEBF是菱形.
(2)由(1)可得,AD=BC,AD=BG,
∴CB=BG,
即B是CG的中点,
又∵F是CD的中点,
∴当CD=CG时,CF=CB,
又∵Rt△BCD中,CF=BF,
∴△BCF是等边三角形,
∴∠C=60°,∠FBG=120°,
∴∠ADC=∠ABC=120°,∠DFB=60°+60°=120°,
∴∠DEB=120°,
∴图中所有与∠C互补的角为∠ADC、∠ABC、∠DFB、∠DEB、∠FBG.
点评 本题主要考查了平行四边形的性质、菱形的判定,直角三角形的性质,解题时注意:在直角三角形中斜边中线等于斜边一半,正确得出ED=BE是解题关键.

练习册系列答案
相关题目
3.在-4、-2、0、1、3、4这六个数中,正数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20. 如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么BF:CF等于( )
如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么BF:CF等于( )
 如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么BF:CF等于( )
如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么BF:CF等于( )| A. | 5:8 | B. | 3:8 | C. | 3:5 | D. | 2:5 |
 如图,等边三角形OAB的边长为2,P是线段OA上任意一点(不含端点O,A),过O、P两点的抛物线和过A,P两点的抛物线的顶点分别在OB,AB上,则这两个二次函数的最大值之和等于$\sqrt{3}$.
如图,等边三角形OAB的边长为2,P是线段OA上任意一点(不含端点O,A),过O、P两点的抛物线和过A,P两点的抛物线的顶点分别在OB,AB上,则这两个二次函数的最大值之和等于$\sqrt{3}$.
 用5个完全相同的小正方体组成如图所示的立体图形,将右上角的小正方体拿掉后俯视图为( )
用5个完全相同的小正方体组成如图所示的立体图形,将右上角的小正方体拿掉后俯视图为( )



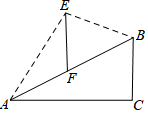 如图,小明家附近有一斜坡AB=40米,其坡度$i=1:\sqrt{3}$,斜坡AB上有一竖直向上的古树EF,小明在山底A处看古树树顶E的仰角为60°,在山顶B处看古树树顶E的仰角为15°,则古树的高约为(参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)( )
如图,小明家附近有一斜坡AB=40米,其坡度$i=1:\sqrt{3}$,斜坡AB上有一竖直向上的古树EF,小明在山底A处看古树树顶E的仰角为60°,在山顶B处看古树树顶E的仰角为15°,则古树的高约为(参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)( )