题目内容
1.下列根式化简后,被开方数与$\sqrt{3}$的被开方数相同的是( )| A. | $\sqrt{24}$ | B. | $\sqrt{18}$ | C. | $-\sqrt{12}$ | D. | $\sqrt{\frac{3}{2}}$ |
分析 根据二次根式化成最简二次根式后,被开方数相同的二次根式叫做同类二次根式,可得答案.
解答 解:A、$\sqrt{24}$=2$\sqrt{6}$与$\sqrt{3}$的被开方数不同,故A错误;
B、$\sqrt{18}$=3$\sqrt{2}$$\sqrt{3}$的被开方数不同,故B错误;
C、-$\sqrt{12}$=-2$\sqrt{3}$$\sqrt{3}$的被开方数相同,故C正确;
D、$\sqrt{\frac{3}{2}}$=$\frac{\sqrt{6}}{2}$$\sqrt{3}$的被开方数不同,故D错误;
故选:C.
点评 此题主要考查了同类二次根式的定义,即:二次根式化成最简二次根式后,被开方数相同的二次根式叫做同类二次根式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.下列说法正确的有( )
①△ABC在平移过程中,对应线段一定平行;
②△ABC在平移过程中,对应线段一定相等;
③△ABC在平移过程中,对应角一定相等;
④△ABC在平移过程中,图形大小不改变.
①△ABC在平移过程中,对应线段一定平行;
②△ABC在平移过程中,对应线段一定相等;
③△ABC在平移过程中,对应角一定相等;
④△ABC在平移过程中,图形大小不改变.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.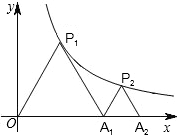 如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )
如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )
 如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )
如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )| A. | -1+$\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | -2+2$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
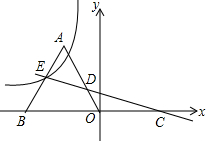 如图,△ABO为等边三角形,点B的坐标为(-4,0),过点C(4,0)作直线l交AO于点D,交AB于点E,点E在反比例函数y=$\frac{k}{x}$ (x<0)的图象上,且△ADE的面积和△DOC的面积相等,则k的值是-3$\sqrt{3}$.
如图,△ABO为等边三角形,点B的坐标为(-4,0),过点C(4,0)作直线l交AO于点D,交AB于点E,点E在反比例函数y=$\frac{k}{x}$ (x<0)的图象上,且△ADE的面积和△DOC的面积相等,则k的值是-3$\sqrt{3}$.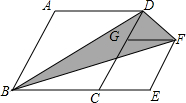 如图,菱形ABCD和菱形CEFG,AB=2,∠A=120°,点G在CD上,点B,C,E在同一条直线上,连接BD,BF,则△BDF的面积为$\sqrt{3}$.
如图,菱形ABCD和菱形CEFG,AB=2,∠A=120°,点G在CD上,点B,C,E在同一条直线上,连接BD,BF,则△BDF的面积为$\sqrt{3}$.