题目内容
6.下列命题中:①任意三点确定一个圆;②平分弦的直径垂直于弦;③相等的弦所对的弧相等;④90°的圆心角所对的弦是直径;⑤同弧或等弧所对的圆周角相等.其中真命题的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 ①在一条直线上的三点就不能确定一个圆故为假命题;
②当弦为直径时不垂直也平分,故为假命题;
③利用弧与弦的定义求解;
④根据圆周角定理的推论进行判断;
⑤根据圆周角定理即可作出判断.
解答 解:①假命题,当三点在同一条直线上时,就不能确定一个圆了;
②假命题,当弦为直径时就不一定垂直了;
③假命题,一条弦对着两条弧,可能不相等;
④真命题;
⑤真命题,同弧或等弧所对的圆周角相等.
故选A.
点评 本题主要考查了确定圆的条件,垂径定理及圆周角定理等圆的一些基本的知识.

练习册系列答案
相关题目
14.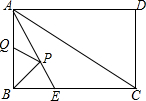 矩形ABCD中,AB=3,BC=4,∠BAC的平分线交BC于E,P、Q分别是AE、AB上的动点,则PB+PQ的最小值是( )
矩形ABCD中,AB=3,BC=4,∠BAC的平分线交BC于E,P、Q分别是AE、AB上的动点,则PB+PQ的最小值是( )
 矩形ABCD中,AB=3,BC=4,∠BAC的平分线交BC于E,P、Q分别是AE、AB上的动点,则PB+PQ的最小值是( )
矩形ABCD中,AB=3,BC=4,∠BAC的平分线交BC于E,P、Q分别是AE、AB上的动点,则PB+PQ的最小值是( )| A. | 5 | B. | $\frac{7}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{12}{5}$ |
1.下列根式化简后,被开方数与$\sqrt{3}$的被开方数相同的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{18}$ | C. | $-\sqrt{12}$ | D. | $\sqrt{\frac{3}{2}}$ |
 如图,是某个反比例函数图象的前一部分,A、B为图象上两点,根据图象.
如图,是某个反比例函数图象的前一部分,A、B为图象上两点,根据图象.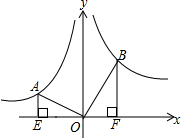 如图,A,B两点分别在反比例函数y=-$\frac{1}{x}$和y=$\frac{k}{x}$的图象上,连接OA、OB,过A、B分别作x轴的垂线,垂足分别为E、F,若OA⊥OB,OB=2OA,则k的值为4.
如图,A,B两点分别在反比例函数y=-$\frac{1}{x}$和y=$\frac{k}{x}$的图象上,连接OA、OB,过A、B分别作x轴的垂线,垂足分别为E、F,若OA⊥OB,OB=2OA,则k的值为4.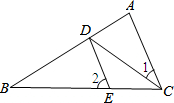 如图,已知CD平分∠ACB,DE∥AC,∠1=20°,则∠2=40°.
如图,已知CD平分∠ACB,DE∥AC,∠1=20°,则∠2=40°. 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数$y=\frac{k+1}{x}$的图象上.若点A的坐标为(-2,-2),则k的值为3.
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数$y=\frac{k+1}{x}$的图象上.若点A的坐标为(-2,-2),则k的值为3.