题目内容
10.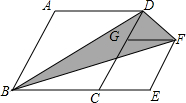 如图,菱形ABCD和菱形CEFG,AB=2,∠A=120°,点G在CD上,点B,C,E在同一条直线上,连接BD,BF,则△BDF的面积为$\sqrt{3}$.
如图,菱形ABCD和菱形CEFG,AB=2,∠A=120°,点G在CD上,点B,C,E在同一条直线上,连接BD,BF,则△BDF的面积为$\sqrt{3}$.
分析 作FM⊥CD于M,作BH⊥CD于H,设CO=m,EF=a,则$\frac{m}{a}$=$\frac{2}{2+a}$,得出m=$\frac{2a}{2+a}$,求出DO=2-CO=$\frac{4}{2+a}$,由三角函数得出BH=$\sqrt{3}$,FM=$\frac{\sqrt{3}}{2}$a,S△BDF=S△BOD+S△DOF=$\frac{1}{2}$DO•BH+$\frac{1}{2}$FM•DO,即可得出结果.
解答 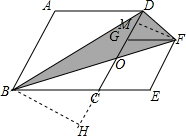 解:作FM⊥CD于M,作BH⊥CD于H,如图所示:
解:作FM⊥CD于M,作BH⊥CD于H,如图所示:
设CO=m,EF=a,
则$\frac{m}{a}$=$\frac{2}{2+a}$,得出m=$\frac{2a}{2+a}$,
∵DO=2-CO=2-$\frac{2a}{2+a}$=$\frac{4}{2+a}$,
BH=BC•sin60°=$\sqrt{3}$,FM=EF•sin60°=$\frac{\sqrt{3}}{2}$a,
∴S△BDF=S△BOD+S△DOF=$\frac{1}{2}$DO•BH+$\frac{1}{2}$FM•DO=$\frac{1}{2}$DO(BH+FM)=$\frac{1}{2}$×$\frac{4}{2+a}$×($\sqrt{3}$+$\frac{\sqrt{3}}{2}$a)=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了菱形的性质、平行线的性质、三角函数、三角形面积的计算方法;熟练掌握菱形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
1.下列根式化简后,被开方数与$\sqrt{3}$的被开方数相同的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{18}$ | C. | $-\sqrt{12}$ | D. | $\sqrt{\frac{3}{2}}$ |
19.使不等式x-4>4x-1成立的值中最大的整数是( )
| A. | 0 | B. | -2 | C. | -1 | D. | 2 |
 如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.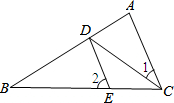 如图,已知CD平分∠ACB,DE∥AC,∠1=20°,则∠2=40°.
如图,已知CD平分∠ACB,DE∥AC,∠1=20°,则∠2=40°.
 如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的值可以是下列选项中的( )
如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的值可以是下列选项中的( ) 如图,E为?ABCD外的一点,AE=DE,BE=CE,AE⊥EC,BE⊥ED,四边形ABCD是矩形吗?请证明你的结论.
如图,E为?ABCD外的一点,AE=DE,BE=CE,AE⊥EC,BE⊥ED,四边形ABCD是矩形吗?请证明你的结论.