题目内容
5.若方程$\frac{x-1}{x+1}$+$\frac{5}{1-x}$=$\frac{m}{{x}^{2}-1}$有增根,则m的值是-10或4.分析 先把分式方程化为整式方程,再令最简公分母=0,求出增根x的值,代入即可求出m的值.
解答 解:$\frac{x-1}{x+1}$+$\frac{5}{1-x}$=$\frac{m}{{x}^{2}-1}$,
去分母得,
(x-1)(1-x)+5(x+1)=-m,
分式方程有增根,则增根会使得(x+1)(1-x)=0,
解得:x=1或x=-1,
把x=1代入可得m=-10,
把x=-1代入可得m=4,
故答案为:-10或4.
点评 此题主要考查分式方程的增根,会把分式方程化为整式方程,会确定分式方程的增根是解题的关键.

练习册系列答案
相关题目
 如图,一次函数y=-$\frac{4}{5}$x+12与x轴、y轴相交于点A、B两点,动点P以4个单位/秒的速度从点O出发,沿OA方向在线段OA上运动,以P为圆心,OP长为半径作⊙P;同时动点E以5个单位/秒的速度从点A出发,沿x轴的负半轴方向运动,过点E作EF⊥x轴,交射线AB于点F,以EF为边在EF的左侧作正方形EFMN,设运动时间为t秒.
如图,一次函数y=-$\frac{4}{5}$x+12与x轴、y轴相交于点A、B两点,动点P以4个单位/秒的速度从点O出发,沿OA方向在线段OA上运动,以P为圆心,OP长为半径作⊙P;同时动点E以5个单位/秒的速度从点A出发,沿x轴的负半轴方向运动,过点E作EF⊥x轴,交射线AB于点F,以EF为边在EF的左侧作正方形EFMN,设运动时间为t秒. 如图,AB为⊙O的直径,点C是$\widehat{AB}$上一点,点D为$\widehat{AC}$的中点,弦AC、BD交于点E,F为BD延长线上一点,且FA是⊙O的切线,
如图,AB为⊙O的直径,点C是$\widehat{AB}$上一点,点D为$\widehat{AC}$的中点,弦AC、BD交于点E,F为BD延长线上一点,且FA是⊙O的切线,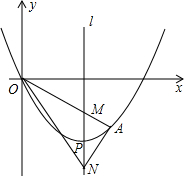 如图,抛物线y=$\frac{1}{4}$(x-4)2-4的顶点为P,M,N均在对称轴上,且PM=PN,延长OM交抛物线于点A,求证:∠ANM=∠ONM.
如图,抛物线y=$\frac{1}{4}$(x-4)2-4的顶点为P,M,N均在对称轴上,且PM=PN,延长OM交抛物线于点A,求证:∠ANM=∠ONM. 如图,点E为正方形ABCD的边CD的中点,点F在AD上,CF交AE于点G,且∠CGE=45°,AE=$\sqrt{5}$,则CF的长为$\frac{2}{3}$$\sqrt{10}$.
如图,点E为正方形ABCD的边CD的中点,点F在AD上,CF交AE于点G,且∠CGE=45°,AE=$\sqrt{5}$,则CF的长为$\frac{2}{3}$$\sqrt{10}$.