题目内容
14.已知y=y1-y2,y1与x成正比例,y2与x-2成反比例,且当x=3时,y=5;当x=1时,y=-1(1)求y与x之间的函数表达式;
(2)当x=4时,求y的值.
分析 (1)根据正比例和反比例函数的定义设表达式,再根据给出自变量和函数的对应值求出待定的系数则可;
(2)将x=4代入(1)中求值即可.
解答 解:(1)设y1=mx,y2=$\frac{n}{x-2}$,
则y=mx-$\frac{n}{x-2}$,
根据题意,得:$\left\{\begin{array}{l}{3m-n=5}\\{m+\frac{1}{2}n=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=\frac{3}{5}}\\{n=-\frac{16}{5}}\end{array}\right.$,
∴y=$\frac{3}{5}$x+$\frac{16}{5x-10}$;
(2)当x=4时,y=$\frac{3}{5}$×4+$\frac{16}{5×4-10}$=$\frac{12}{5}$+$\frac{8}{5}$=4.
点评 考查了待定系数法的应用,解决本题的关键是得到y与x的函数关系式,需注意两个函数的比例系数是不同的.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
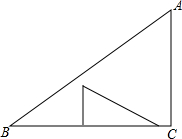 在△ABC中,∠C=90°,AC=3,BC=4,两直角边分别为1,2的三角形纸片按如图所示放置,若该纸片在△ABC内任意平移,求△ABC内不能被平移到的部分的面积和.
在△ABC中,∠C=90°,AC=3,BC=4,两直角边分别为1,2的三角形纸片按如图所示放置,若该纸片在△ABC内任意平移,求△ABC内不能被平移到的部分的面积和.