��Ŀ����
15�� ��ͼ��һ�κ���y=-$\frac{4}{5}$x+12��x�ᡢy���ཻ�ڵ�A��B���㣬����P��4����λ/����ٶȴӵ�O��������OA�������߶�OA���˶�����PΪԲ�ģ�OP��Ϊ�뾶����P��ͬʱ����E��5����λ/����ٶȴӵ�A��������x��ĸ����᷽���˶�������E��EF��x�ᣬ������AB�ڵ�F����EFΪ����EF�������������EFMN�����˶�ʱ��Ϊt�룮
��ͼ��һ�κ���y=-$\frac{4}{5}$x+12��x�ᡢy���ཻ�ڵ�A��B���㣬����P��4����λ/����ٶȴӵ�O��������OA�������߶�OA���˶�����PΪԲ�ģ�OP��Ϊ�뾶����P��ͬʱ����E��5����λ/����ٶȴӵ�A��������x��ĸ����᷽���˶�������E��EF��x�ᣬ������AB�ڵ�F����EFΪ����EF�������������EFMN�����˶�ʱ��Ϊt�룮��1�����A���B�����ꣻ
��2������BP��PM����tΪ��ֵʱ��BP=PM��
��3����ֱ��BM������P��ֱ��BM����ʱ����������EFMN�ı߳���
���� ��1����ֵ������ݣ���������������꣬
��2��BP�������Ƕ���ֵ�������������ʱ��t��
��3����ȷ����ֱ��BM����ʽ����BM��ԲP���У�����������Ǻ�������������⼴�ɣ�
��� �⣺��1����һ�κ���y=-$\frac{4}{5}$x+12��x�ᡢy���ཻ�ڵ�A��B���㣬
��y=0��
��0=-$\frac{4}{5}$x+12��
��x=15��
��A��15��0��
��x=0��y=12��
��B��0��12��
��2�����˶��У�OP=4t��AE=5t��EF=EN=4t��
��AN=9t��
��P��4t��0����M��15-9t��4t����
��PM=$\sqrt{��15-9t-4t��^{2}+��4t��^{2}}$��
BP=$\sqrt{��4t��^{2}+144}$��
��BP=PM��BP=$\sqrt{��4t��^{2}+144}$��
��$\sqrt{��15-9t-4t��^{2}+��4t��^{2}}$=$\sqrt{��4t��^{2}+144}$��
��$t=\frac{3}{13}$����$t=\frac{27}{13}$
��3�����˶��ã�P��4t��0����M��15-9t��4t����
��B��0��12����
��ֱ��BM�Ľ���ʽΪy=$\frac{4t-12}{15-9t}$x+12��
��ֱ��BM��x��Ľ���GΪ��$\frac{3��9t-15��}{t-3}$��0����
����P��ֱ��BM����ʱ��
�ٵ���G��O�غ�ʱ������$\frac{3��9t-15��}{t-3}$=0
��t=$\frac{5}{3}$��
����ͼ��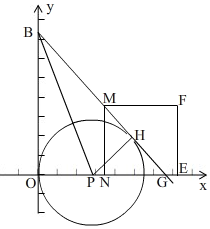 ��BP�ǡ�OBG�Ľ�ƽ���ߣ�
��BP�ǡ�OBG�Ľ�ƽ���ߣ�
����P��PH��BM��H��
��PH=OP=4t��
��P��4t��0����G��$\frac{3��9t-15��}{t-3}$��0����
��PG=$\frac{3��9t-15��}{t-3}$-4t��
��Rt��PHG��sin��PGH=$\frac{PH}{PG}$��
��Rt��BOG��sin��OGB=$\frac{OB}{BG}$��
��$\frac{PH}{PG}=\frac{OB}{BG}$
��$\frac{B{O}^{2}}{O{P}^{2}}=\frac{B{G}^{2}}{P{G}^{2}}$��
��BG2=[$\frac{3��9t-15��}{t-3}$]2+144��PG2=[$\frac{3��9t-15��}{t-3}$-4t]2��BO2=144��OP2=16t2��
��$\frac{144}{16{t}^{2}}$=$\frac{[\frac{3��9t-15��}{t-3}]^{2}+144}{[\frac{3��9t-15��}{t-3}-4t]^{2}}$��
��t=1����t=$\frac{5}{3}$���ᣩ��t=-5���ᣩ��
����t=1��t=$\frac{5}{3}$ʱ����P��BM���У�
����������EFMN�ı߳�=4t=4��$\frac{20}{3}$��
���� ������Բ���ۺ��⣬��Ҫ������ƽ������ϵ�������ľ��빫ʽ��������Ǻ������Ȿ��Ĺؼ�����ʱ��t��ʾ���������߶Σ�

 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�| A�� | 0 | B�� | 1 | C�� | -1 | D�� | ��1 |
 ��ͼΪij���������ͼ����ͼ���������������ǣ�������
��ͼΪij���������ͼ����ͼ���������������ǣ�������| A�� | ���� | B�� | ˫�㵰�� | C�� | ��ӾȦ | D�� | Ǧ�� |
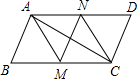 ��ͼ����?ABCD�У�AM��CN�ֱ��ǡ�BAD�͡�BCD��ƽ���ߣ�����һ�������������ж��ı���AMCNΪ���ε��ǣ�������
��ͼ����?ABCD�У�AM��CN�ֱ��ǡ�BAD�͡�BCD��ƽ���ߣ�����һ�������������ж��ı���AMCNΪ���ε��ǣ�������| A�� | AM=AN | B�� | MN��AC | ||
| C�� | MN�ǡ�AMC��ƽ���� | D�� | ��BAD=120�� |
 ij��������������A��B��C��ͬһ��·�ϣ��ס��������οʹӾ���A�������ײ��е�����C���ҳ˾����۹�ȵ�����B����B��ͣ��һ��ʱ����ٲ��е�����C���ס��������뿪����A���·��S���ף�����ʱ��t�����ӣ��ĺ���ͼ����ͼ��ʾ��
ij��������������A��B��C��ͬһ��·�ϣ��ס��������οʹӾ���A�������ײ��е�����C���ҳ˾����۹�ȵ�����B����B��ͣ��һ��ʱ����ٲ��е�����C���ס��������뿪����A���·��S���ף�����ʱ��t�����ӣ��ĺ���ͼ����ͼ��ʾ��
 ��ͼ��ijУ�ڿ�չ���������ͼ������������ļ�ֵ�۵Ļ�У�С��ͬѧ���Լ���Ҫ��ǿ�ġ��������������ơ��������Ρ��������š��ļ�ֵȡ�����ֱַ�����4���ʵء���С��ȫһ����Ӳֽ���ϣ��Ƴɿ�Ƭ����ʱ�����Լ�Ҫ��������ط��ĺ�ѧ����С��ͬѧ���ѿ�Ƭ���һ����ѧ�⿼ͬ��С��������4�ſ�Ƭϴ�Ⱥ��泯�Ϸ��������ϣ����������ȡһ�ſ�Ƭ�����Żأ��������ȡ��һ�ſ�Ƭ����С��ͬѧ���б�������״ͼ����������γ鵽��Ƭ�ϵ����ֺ��С��������������š���ֵȡ��ĸ��ʣ���Ƭ���ƿ�����ĸ��ʾ����
��ͼ��ijУ�ڿ�չ���������ͼ������������ļ�ֵ�۵Ļ�У�С��ͬѧ���Լ���Ҫ��ǿ�ġ��������������ơ��������Ρ��������š��ļ�ֵȡ�����ֱַ�����4���ʵء���С��ȫһ����Ӳֽ���ϣ��Ƴɿ�Ƭ����ʱ�����Լ�Ҫ��������ط��ĺ�ѧ����С��ͬѧ���ѿ�Ƭ���һ����ѧ�⿼ͬ��С��������4�ſ�Ƭϴ�Ⱥ��泯�Ϸ��������ϣ����������ȡһ�ſ�Ƭ�����Żأ��������ȡ��һ�ſ�Ƭ����С��ͬѧ���б�������״ͼ����������γ鵽��Ƭ�ϵ����ֺ��С��������������š���ֵȡ��ĸ��ʣ���Ƭ���ƿ�����ĸ��ʾ����